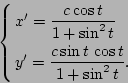Klaas Pieter Hart
Oktober, 1999
Het woord lemniscaat komt, hoe kan het anders, uit het Latijn
en wel van lemniscatus wat `versierd met linten' betekent;
en inderdaad, een lemniscaat lijkt wel een beetje op een strikje
(zonder de losse uiteinden).
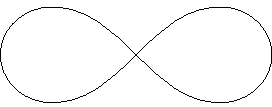
Deze leniscaat is op een paar manieren te beschrijven.
De eerste manier lijkt een beetje op de definitie van een ellips,
met het woord `som' vervangen door het woord `produkt'.
Neem een getal ![]() en daarbij de punten
en daarbij de punten
![]() en
en
![]() in het vlak;
de lemniscaat met brandpunten
in het vlak;
de lemniscaat met brandpunten ![]() en
en ![]() is de verzameling van die punten
is de verzameling van die punten ![]() met
met
![]() .
.
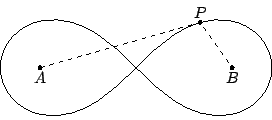
De lemniscaat kun je ook maken door een hyperbool in een cirkel te
spiegelen.
Spiegelen in een cirkel met middelpunt ![]() en straal
en straal ![]() gaat als volgt:
trek vanuit
gaat als volgt:
trek vanuit ![]() de halve lijn door je punt
de halve lijn door je punt ![]() , het spiegelbeeld van
, het spiegelbeeld van ![]() ten
opzichte van de cirkel is het punt
ten
opzichte van de cirkel is het punt ![]() op de halve lijn met
op de halve lijn met
![]() .
.
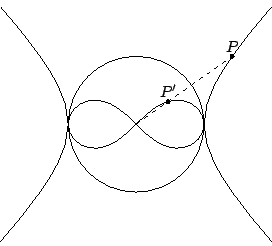
Voor onze lemniscaat nemen we de cirkel om ![]() met straal
met straal ![]() en de
hyperbool met vergelijking
en de
hyperbool met vergelijking ![]() .
De hyperbool heeft een mooie parametrisering:
.
De hyperbool heeft een mooie parametrisering:
Het spiegelpunt van ![]() ten opzichte van de cirkel is vrij eenvoudig
te vinden: bedenk dat
ten opzichte van de cirkel is vrij eenvoudig
te vinden: bedenk dat ![]() een veelvoud van
een veelvoud van ![]() moet zijn.
We vinden dan dat
moet zijn.
We vinden dan dat ![]() de volgende coördinaten heeft:
de volgende coördinaten heeft:
![]() en
en
![]() .
Voor de punten op de hyperbool levert dit:
.
Voor de punten op de hyperbool levert dit: