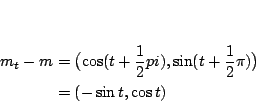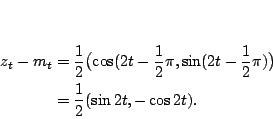Next: Met licht
Up: De Cardioïde
Previous: De Cardioïde
Cardioïden komen heel vaak voor; we geven twee voorbeelden.
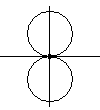
Neem twee cirkels met diameter 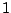 en leg ze zó neer dat ze de
en leg ze zó neer dat ze de 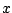 -as in de
oorsprong raken -- de een van onderen de ander van boven.
-as in de
oorsprong raken -- de een van onderen de ander van boven.
Laat nu de bovenste cirkel (zonder slippen) langs de onderste cirkel rollen;
het punt dat in het begin in de oorsprong lag beschrijft nu precies onze
cardioïde.
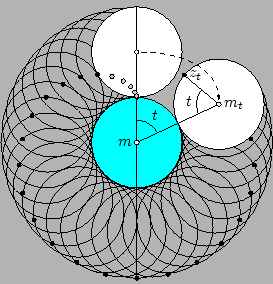
In het plaatje is de bovenste cirkel over een hoek van 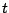 gedraaid;
met middelpunt ligt nu in
gedraaid;
met middelpunt ligt nu in 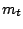 en het punt dat in de oorsprong begon ligt
nu in
en het punt dat in de oorsprong begon ligt
nu in 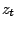 .
Je kunt nu uitrekenen dat
.
Je kunt nu uitrekenen dat
(in het plaatje is 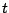 negatief, we gaan immers met de klok mee)
en dat
negatief, we gaan immers met de klok mee)
en dat
Nu kunnen we de coördinaten van 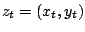 uitrekenen:
uitrekenen:
Je kunt controleren of dit punt op de cardioïde ligt door deze waarden
in de 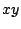 -vergelijking in te vullen.
Hieronder zie je
-vergelijking in te vullen.
Hieronder zie je 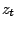 voor een aantal waarden van
voor een aantal waarden van 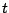 .
.



Next: Met licht
Up: De Cardioïde
Previous: De Cardioïde
KP Hart
2006-04-06
![]() en leg ze zó neer dat ze de
en leg ze zó neer dat ze de ![]() -as in de
oorsprong raken -- de een van onderen de ander van boven.
-as in de
oorsprong raken -- de een van onderen de ander van boven.