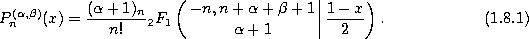
Definition.
Orthogonality.
Recurrence relation.
Normalized recurrence relation.
where
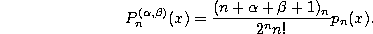
Differential equation.
Forward shift operator.
Backward shift operator.
or equivalently
Rodrigues-type formula.
Generating functions.
Remarks. The Jacobi polynomials defined by (1.8.1) and the Meixner polynomials given by (1.9.1) are related in the following way :
The Jacobi polynomials are also related to the Gegenbauer (or ultraspherical) polynomials defined by (1.8.15) by the quadratic transformations :
and
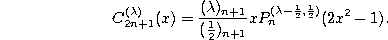
References. [2], [3], [10], [12], [18], [31], [34], [35], [36], [37], [38], [39], [40], [43], [46], [47], [48], [49], [61], [64], [75], [89], [95], [108], [110], [114], [123], [126], [127], [130], [137], [138], [139], [145], [150], [153], [154], [158], [171], [174], [175], [176], [177], [178], [179], [180], [181], [182], [183], [184], [194], [197], [201], [202], [209], [211], [213], [214], [215], [221], [227], [231], [254], [260], [264], [265], [266], [267], [269], [270], [273], [274], [286], [287], [290], [301], [302], [308], [309], [311], [314], [315], [318], [320], [323], [329], [333], [334], [335], [337], [342], [354], [360], [369], [374], [376], [377], [380], [382], [386], [388], [390], [393], [403], [405], [407], [408].
Definition. The Gegenbauer (or ultraspherical) polynomials are Jacobi
polynomials with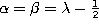 
and another normalization :
Orthogonality.
Recurrence relation.
Normalized recurrence relation.
where
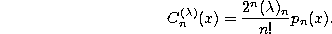
Differential equation.
Forward shift operator.
Backward shift operator.
or equivalently
Rodrigues-type formula.
Generating functions.
Remarks.
The case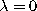 
needs another normalization. In that case we have the
Chebyshev polynomials of the first kind described in the next subsection.
The Gegenbauer (or ultraspherical) polynomials defined by (1.8.15) and the Jacobi polynomials given by (1.8.1) are related by the quadratic transformations :
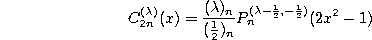
and
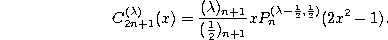
References. [2], [4], [33], [38], [39], [43], [46], [57], [82], [86], [88], [89], [90], [95], [98], [99], [100], [102], [103], [108], [123], [129], [131], [135], [139], [140], [141], [147], [148], [151], [154], [157], [174], [180], [186], [202], [214], [274], [289], [306], [310], [314], [321], [323], [354], [360], [361], [368], [376], [388], [390], [395], [408].
Definitions. The Chebyshev polynomials of the first kind can be obtained
from the Jacobi polynomials by taking 
:
and the Chebyshev polynomials of the second kind can be obtained from the
Jacobi polynomials by taking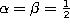 
:
Orthogonality.
Recurrence relations.
Normalized recurrence relations.
where
where
Differential equations.
Forward shift operator.
Backward shift operator.
or equivalently
Rodrigues-type formulas.
Generating functions.
Remarks. The Chebyshev polynomials can also be written as :
and
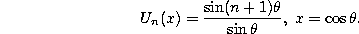
Further we have
where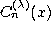 
denotes the Gegenbauer (or ultraspherical)
polynomial defined by (1.8.15) in the preceding subsection.
References. [2], [46], [51], [52], [78], [123], [131], [140], [154], [202], [211], [311], [314], [323], [360], [362], [367], [388], [390], [401], [408].
Definition. The Legendre (or spherical) polynomials are Jacobi
polynomials with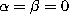 
:
Orthogonality.
Recurrence relation.
Normalized recurrence relation.
where
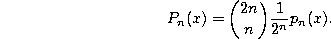
Differential equation.
Rodrigues-type formula.
Generating functions.
References. [2], [5], [13], [85], [89], [105], [123], [131], [140], [152], [154], [202], [314], [323], [329], [360], [388], [390], [408].
