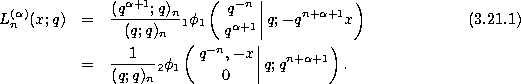
Definition.
Orthogonality. The q-Laguerre polynomials satisfy two kinds of orthogonality relations, an absolutely continuous one and a discrete one. These orthogonality relations are given by, respectively :
and
Recurrence relation.
Normalized recurrence relation.
where
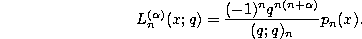
q-Difference equation.
where

Forward shift operator.
or equivalently
Backward shift operator.
or equivalently
where
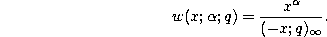
Rodrigues-type formula.
Generating functions.
Remarks. The q-Laguerre polynomials are sometimes called the generalized Stieltjes-Wigert polynomials.
If we change q to 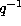 we obtain the little q-Laguerre
(or Wall) polynomials given by (3.20.1) in the following
way :
we obtain the little q-Laguerre
(or Wall) polynomials given by (3.20.1) in the following
way :

The q-Laguerre polynomials defined by (3.21.1) and the alternative q-Charlier polynomials given by (3.22.1) are related in the following way :
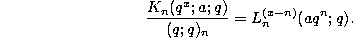
The q-Laguerre polynomials defined by (3.21.1) and the q-Charlier polynomials given by (3.23.1) are related in the following way :
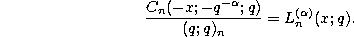
Since the Stieltjes and Hamburger moment problems corresponding to the q-Laguerre polynomials are indeterminate there exist many different weight functions.
References. [11], [13], [42], [43], [64], [71], [116], [121], [123], [124], [156], [193], [203], [235], [246], [319].