Taylor series

>    restart:

Se e: Stewart, chapter 11. Maple can find the Taylor series of a function, such as for instance:

 

>    taylor(exp(x),x=0);

series(1+1*x+1/2*x^2+1/6*x^3+1/24*x^4+1/120*x^5+O(x^6),x,6)

Standard Maple gives the answer till the order:  

>    Order;

6

We can eventually change this by explicitly entering the wanted order:

>    taylor(exp(x),x=0,10);

series(1+1*x+1/2*x^2+1/6*x^3+1/24*x^4+1/120*x^5+1/720*x^6+1/5040*x^7+1/40320*x^8+1/362880*x^9+O(x^10),x,10)

Or by changing the value of Order  first:

>    Order:=12: taylor(exp(x),x=0);

series(1+1*x+1/2*x^2+1/6*x^3+1/24*x^4+1/120*x^5+1/720*x^6+1/5040*x^7+1/40320*x^8+1/362880*x^9+1/3628800*x^10+1/39916800*x^11+O(x^12),x,12)

We change Order  again to its default value and try to find a Taylor series about x=1 :

>    Order:=6: taylor(exp(x),x=1);

series(exp(1)+exp(1)*(x-1)+1/2*exp(1)*(x-1)^2+1/6*exp(1)*(x-1)^3+1/24*exp(1)*(x-1)^4+1/120*exp(1)*(x-1)^5+O((x-1)^6),x=-(-1),6)

By using Maple we can easily check the Taylor series on the formulae sheet (also see: Stewart, § 11.10):

>    exp(x)=taylor(exp(x),x=0,4);

>    sin(x)=taylor(sin(x),x=0,8);

>    cos(x)=taylor(cos(x),x=0,8);

>    ln(1+x)=taylor(ln(1+x),x=0,5);

>    (1+x)^k=taylor((1+x)^k,x=0,4);

exp(x) = series(1+1*x+1/2*x^2+1/6*x^3+O(x^4),x,4)

sin(x) = series(1*x-1/6*x^3+1/120*x^5-1/5040*x^7+O(x^8),x,8)

cos(x) = series(1-1/2*x^2+1/24*x^4-1/720*x^6+O(x^8),x,8)

ln(x+1) = series(1*x-1/2*x^2+1/3*x^3-1/4*x^4+O(x^5),x,5)

(x+1)^k = series(1+k*x+1/2*k*(k-1)*x^2+1/6*k*(k-1)*(k-2)*x^3+O(x^4),x,4)

Example 6 of § 11.10:

>    taylor(x*cos(x),x=0);

series(1*x-1/2*x^3+1/24*x^5+O(x^7),x,7)

Example 7 of § 11.10:

>    taylor(sin(x),x=Pi/3);

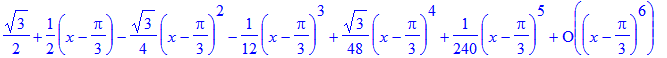
series(1/2*3^(1/2)+1/2*(x-1/3*Pi)+(-1/4*3^(1/2))*(x-1/3*Pi)^2-1/12*(x-1/3*Pi)^3+1/48*3^(1/2)*(x-1/3*Pi)^4+1/240*(x-1/3*Pi)^5+O((x-1/3*Pi)^6),x=-(-1/3*Pi),6)

More examples (see: Stewart, § 11.10):

>    1/(1-x)=taylor(1/(1-x),x=0);

>    arctan(x)=taylor(arctan(x),x=0);

>    exp(x)*sin(x)=taylor(exp(x)*sin(x),x=0);

>    tan(x)=taylor(tan(x),x=0);

1/(1-x) = series(1+1*x+1*x^2+1*x^3+1*x^4+1*x^5+O(x^6),x,6)

arctan(x) = series(1*x-1/3*x^3+1/5*x^5+O(x^6),x,6)

exp(x)*sin(x) = series(1*x+1*x^2+1/3*x^3-1/30*x^5+O(x^6),x,6)

tan(x) = series(1*x+1/3*x^3+2/15*x^5+O(x^6),x,6)

Example 1 of § 11.11:

>    1/(1+x)^2=taylor(1/(1+x)^2,x=0);

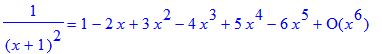
1/((x+1)^2) = series(1-2*x+3*x^2-4*x^3+5*x^4-6*x^5+O(x^6),x,6)

This is an example of a binomial series , where the following binomial coefficients arise:

>    for n from 0 to 5 do binomial(-2,n) od;

1

-2

3

-4

5

-6

Example 2 of § 11.11:

>    1/sqrt(4-x)=taylor(1/sqrt(4-x),x=0);

1/((4-x)^(1/2)) = series(1/2+1/16*x+3/256*x^2+5/2048*x^3+35/65536*x^4+63/524288*x^5+O(x^6),x,6)

If we write 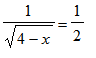  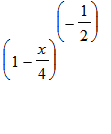1/sqrt(4-x) = 1/2  * (1-x/4)^(-1/2)   , then we obtain:

>    1/sqrt(4-x)=1/2*taylor((1-x/4)^(-1/2),x=0);

1/((4-x)^(1/2)) = 1/2*(series(1+1/8*x+3/128*x^2+5/1024*x^3+35/32768*x^4+63/262144*x^5+O(x^6),x,6))

Here the following binomial coefficients arise:

>    for n from 0 to 5 do binomial(-1/2,n) od;

1

-1/2

3/8

-5/16

35/128

-63/256

>