Impliciet differentiŽren
| > | restart: |
Z ie: Stewart, ß 3.6. We beginnen met het folium van Descartes uit voorbeeld 2:
| > | folium:=x^3+y^3=6*x*y; |
![]()
Om de grafiek te kunnen plotten maken we gebruik van het commando implicitplot uit het pakket plots . We laden daarom eerst het pakket plots (vervang eventueel de dubbele punt door een puntkomma om de inhoud van het pakket te zien):
| > | with(plots): |
Vervolgens kunnen we gebruikmaken van de commando's uit het pakket plots , waaronder het commando implicitplot (met behulp van numpoints kan de kwaliteit van het plaatje worden verhoogd):
| > | implicitplot(folium,x=-4..4,y=-4..4,numpoints=10000); |
![[Maple Plot]](images/ImplicietDifferentieren2.gif)
Om nu y'=dy/dx te kunnen bepalen differentiŽren we naar x , waarbij we y als functie van x opvatten. Dit kunnen we Maple vertellen door y expliciet als y(x) in te voeren:
| > | diff(x^3+(y(x))^3=6*x*y(x),x); |
![]()
of zo:
| > | diff(subs(y=y(x),folium),x); |
![]()
Hieruit volgt dat y'=(6y-3x^2)/(3y^2-6x) oftewel: y'=(2y-x^2)/(y^2-2x) . In Maple kan dit echter ook rechtstreeks met het commando implicitdiff :
| > | rico:=implicitdiff(folium,y,x); |
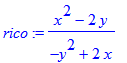
We vinden nu de richtingscoŽfficiŽnt van de raaklijn in het punt (3,3) door x=3 en y=3 te substitueren:
| > | r:=subs(x=3,y=3,rico); |
![]()
De raaklijn in het punt (3,3) is dus gelijk aan: y=-(x-3)+3 oftewel y=-x+6 . Deze kan met behulp van het commando plot worden getekend.
Om nu het folium van Descartes samen met deze raaklijn in ťťn figuur te kunnen tekenen, kunnen we gebruik maken van:
| > | implicitplot({folium,y-3=r*(x-3)},x=-4..4,y=-4..4,numpoints=10000); |
![[Maple Plot]](images/ImplicietDifferentieren7.gif)
We kunnen echter ook verschillende soorten plots combineren met behulp van het commando display (ook onderdeel van het pakket plots ). Daartoe definiŽren we eerst de twee plaatjes (waarbij we de uitvoer onderdrukken), waarna we ze in ťťn figuur tonen:
| > | P1:=implicitplot(folium,x=-4..4,y=-4..4,numpoints=10000): |
| > | P2:=plot(3+r*(x-3),x=-4..4,y=-4..4): |
| > | display(P1,P2); |
![[Maple Plot]](images/ImplicietDifferentieren8.gif)
Vervolgens zoeken we de punten (x,y) op de grafiek waar de raaklijn horizontaal is. Dit zijn de punten (x,y) waarvoor dy/dx=0 . Dus:
| > | fsolve({rico=0,folium},{x,y}); |
![]()
Evenzo voorbeeld 3:
| > | C:=sin(x+y)=y^2*cos(x); |
![]()
| > | implicitplot(C,x=-2..2,y=-2..2); |
![[Maple Plot]](images/ImplicietDifferentieren11.gif)
| > | implicitdiff(C,y,x); |
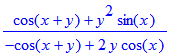
En opgave 27:
| > | cardio:=x^2+y^2=(2*x^2+2*y^2-x)^2; |
![]()
| > | implicitplot(cardio,x=-1..1,y=-1..1,numpoints=10000); |
![[Maple Plot]](images/ImplicietDifferentieren14.gif)
| > | rico:=implicitdiff(cardio,y,x); |
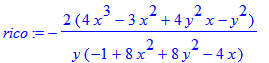
| > | r:=subs(x=0,y=1/2,rico); |
![]()
| > | P1:=implicitplot(cardio,x=-1..1,y=-1..1,numpoints=10000): |
| > | P2:=plot(1/2+r*x,x=-1..1,y=-1..1): |
| > | display(P1,P2); |
![[Maple Plot]](images/ImplicietDifferentieren17.gif)
Tenslotte kijken we nog naar opgave 33:
| > | fancy:=y*(y^2-1)*(y-2)=x*(x-1)*(x-2); |
![]()
| > | implicitplot(fancy,x=-1..3,y=-3..3,numpoints=10000); |
![[Maple Plot]](images/ImplicietDifferentieren19.gif)
| > | rico:=implicitdiff(fancy,y,x); |
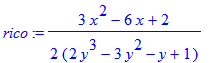
De raaklijn aan de grafiek is horizontaal als de richtingscoŽfficiŽnt gelijk is aan nul:
| > | opl:=solve(rico=0,x); |
![]()
| > | evalf(%); |
![]()
Er zijn dus twee waarden van x waarvoor dit optreedt. De bijbehorende y -coŲrdinaten zijn oplossingen van een vierdegraads vergelijking. Deze kunnen niet eenvoudig exact worden gevonden, maar wel bij benadering (numeriek). Hierbij helpen we Maple een handje door aan te geven waar gezocht moet worden:
| > | fsolve({rico=0,fancy},{x,y},x=0..0.5,y=-2..-0.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=0..0.5,y=-0.5..0.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=0..0.5,y=0.5..1.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=0..0.5,y=1.5..2.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=1..2,y=-2..-0.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=1..2,y=-0.5..0.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=1..2,y=0.5..1.5); |
![]()
| > | fsolve({rico=0,fancy},{x,y},x=1..2,y=1.5..2.5); |
![]()
Voor de raaklijnen aan de grafiek in de punten (0,1) en (0,2) bepalen we eerst de richtingscoŽfficiŽnten in deze punten:
| > | r1:=subs(x=0,y=1,rico);r2:=subs(x=0,y=2,rico); |
![]()
![]()
In ťťn figuur:
| > | implicitplot({fancy,y-1=r1*x,y-2=r2*x},x=-1..3,y=-3..3,numpoints=10000); |
![[Maple Plot]](images/ImplicietDifferentieren33.gif)
| > |