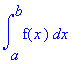
Integralen
| > | restart: |
Z ie: Stewart, hoofdstuk 5. Een integraal wordt in Maple ingevoerd als:
| > | integrate(f(x),x=a..b); |
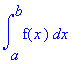
of kortweg als:
| > | int(f(t),t=a..b); |
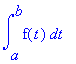
De hoofdstelling van de integraalrekening (zie: Stewart, § 5.3) is dan:
| > | g:=x->int(f(t),t=a..x); |
| > | diff(g(x),x); |
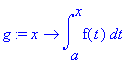
![]()
Maple heeft dan ook geen enkele moeite met (bijvoorbeeld) de opgaven 11 en 15 van § 5.3:
| > | F:=x->int(cos(t^2),t=x..2); |
| > | diff(F(x),x); |
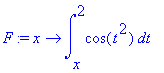
![]()
| > | y:=Int(cos(t)/t,t=3..sqrt(x)); |
| > | diff(y,x); |

![]()
Merk op dat hierbij de kettingregel correct is toegepast:
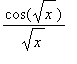 *
*
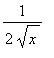 =
=
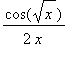 .
.
Maple beschikt standaard over functies zoals Si(x) , de sine integral (zie: Stewart, § 5.3, opgave 58):
| > | int(sin(t)/t,t=0..x); |
![]()
Deze functie kunnen we dan ook eenvoudig plotten:
| > | plot(Si(x),x=-25..25); |
![[Maple Plot]](images/Integralen13.gif)
Het maximum van deze functie wordt blijkbaar aangenomen op het interval (0,5) . De afgeleide moet dan gelijk aan nul zijn:
| > | fsolve(diff(Si(x),x)=0,x=0..5); |
![]()
Dit lijkt op Pi en dat is het natuurlijk ook, want de afgeleide van Si(x) is immers gelijk aan:
| > | Diff(Si(x),x)=diff(Si(x),x); |
![]()
De lokale maxima en minima van Si(x) worden dus (afwisselend) aangenomen in de nulpunten van sin(x) met uitzondering van x=0 .
Een buigpunt ( reflection point ) wordt aangenomen in die x waarvoor de tweede afgeleide gelijk aan nul is:
| > | secder:=diff(Si(x),x$2); |
| > | fsolve(secder=0,x=0..5); |
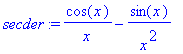
![]()
Dit is dus een oplossing van x*cos(x)-sin(x)=0 oftewel van x=tan(x) .
Hieraan is gemakkelijk te zien dat deze oplossing dus niet uniek is. Immers:
| > | y:='y': |
| > | plot({tan(x), x}, x = -4*Pi..4*Pi, y=-4*Pi..4*Pi, discont = true); |
![[Maple Plot]](images/Integralen18.gif)
N.B.: Omdat we hierboven
y
hadden gedefinieerd als
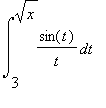 , kunnen we
y
niet zomaar in een andere context gebruiken.
, kunnen we
y
niet zomaar in een andere context gebruiken.
Het volgende snijpunt kunnen we nu ook eenvoudig vinden:
| > | fsolve(secder=0,x=5..10); |
![]()
In opgave 58 van § 5.3 wordt ten slotte nog gevraagd een benadering van
x
te bepalen waarvoor
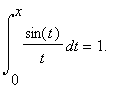 Dus:
Dus:
| > | fsolve(Si(x)=1,x); |
![]()
Laten we nu eens kijken naar de voorbeelden van § 5.5 van Stewart:
| > | Int(x^3*cos(x^4+2),x)=int(x^3*cos(x^4+2),x); |
![]()
Merk op dat Maple de integratieconstante achterwege laat. Maple geeft dus slechts één primitieve in plaats van de verzameling van alle primitieven! We kunnen echter eenvoudig zelf die constante toevoegen.
| > | Int(sqrt(2*x+1),x)=int(sqrt(2*x+1),x); |
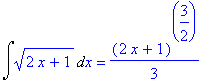
| > | Int(x/sqrt(1-4*x^2),x)=int(x/sqrt(1-4*x^2),x); |
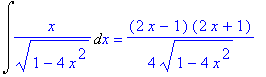
| > | Int(exp(5*x),x)=int(exp(5*x),x); |
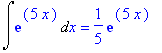
| > | Int(sqrt(1+x^2)*x^5,x)=int(sqrt(1+x^2)*x^5,x); |
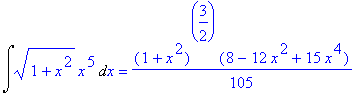
Dit ziet er een beetje anders uit dan de uitkomst in het boek. Echter:
| > | simplify(rhs(%)-1/7*(1+x^2)^(7/2)+2/5*(1+x^2)^(5/2)-1/3*(1+x^2)^(3/2)); |
![]()
Het is dus hetzelfde.
Nog zo'n voorbeeld: we zien eenvoudig in dat
 =
=
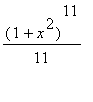 . Maple komt echter met een ander resultaat:
. Maple komt echter met een ander resultaat:
| > | Int(2*x*(1+x^2)^(10),x)=int(2*x*(1+x^2)^(10),x); |
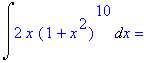
![]()
Maple werkt blijkbaar eerst
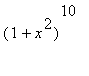 uit en gaat vervolgens termsgewijs integreren. Ook nu kunnen we gemakkelijk zien dat beide uitkomsten correct zijn:
uit en gaat vervolgens termsgewijs integreren. Ook nu kunnen we gemakkelijk zien dat beide uitkomsten correct zijn:
| > | simplify(1/11*(1+x^2)^11-int(2*x*(1+x^2)^10,x)); |
![]()
Beide uitkomsten verschillen dus een constante.
Nu voorbeeld 6 van § 5.5 van Stewart:
| > | Int(tan(x),x)=int(tan(x),x); |
![]()
Hier moeten we even oppassen, want
ln(x)
is slechts gedefinieerd voor
x>0
. Beter is daarom:
 zoals in het boek staat. Toch gaat Maple er wel goed mee om, zoals we kunnen zien aan de volgende voorbeelden. Op het interval
(1/4*Pi,1/3*Pi)
is
tan(x)>0
en ook
cos(x)>0
en op het interval
(2/3*Pi,3/4*Pi)
is
tan(x)<0
en ook
cos(x)<0
:
zoals in het boek staat. Toch gaat Maple er wel goed mee om, zoals we kunnen zien aan de volgende voorbeelden. Op het interval
(1/4*Pi,1/3*Pi)
is
tan(x)>0
en ook
cos(x)>0
en op het interval
(2/3*Pi,3/4*Pi)
is
tan(x)<0
en ook
cos(x)<0
:
| > | Int(tan(x),x=1/4*Pi..1/3*Pi)=int(tan(x),x=1/4*Pi..1/3*Pi); |
| > | Int(tan(x),x=2/3*Pi..3/4*Pi)=int(tan(x),x=2/3*Pi..3/4*Pi); |
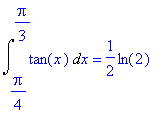
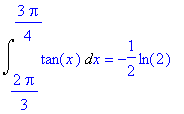
Dit heeft te maken met de (uitgebreide) definitie van ln(x) in Maple, maar we gaan daar niet dieper op in.
Als laatste voorbeeld kijken we naar opgave 3 van de Problems Plus van hoofdstuk 5 van Stewart.
Er wordt gevraagd aan te tonen dat:
![]() <
<
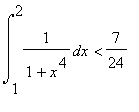
Maple kan de integraal overigens exact berekenen:
| > | Int(1/(1+x^4),x=1..2)=simplify(int(1/(1+x^4),x=1..4)); |
| > | evalf(rhs(%)); |
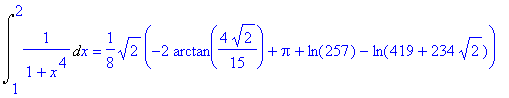
![]()
De functie
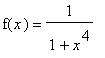 is dalend op het interval
(1,2)
. Verder geldt:
is dalend op het interval
(1,2)
. Verder geldt:
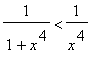 . Dus:
. Dus:
f(2) <
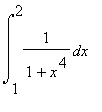 <
<
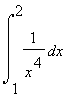 .
Oftewel:
.
Oftewel:
![]() <
<
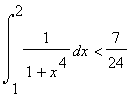 . Want:
. Want:
| > | 1/(1+2^4); |
| > | int(1/x^4,x=1..2); |
![]()
![]()
| > |