De inverse trigonometrische functies
| > | restart: |
Met het commando restart wordt het geheugen van Maple geheel gewist. Zo beginnen we met een schone lei.
In Maple zijn de inverse trigonometrische functies (zie: Stewart, § 1.6) standaard ingebouwd.
Kijk maar eens naar voorbeeld 13 van § 1.6:
| > | arcsin(1/2); |
![]()
Let op het verschil tussen arcsin(1/2) en arcsin(0.5) :
| > | arcsin(0.5); |
![]()
En verder:
| > | tan(arcsin(1/3)); |
![]()
Ook voorbeeld 14 van § 1.6 levert geen probleem op voor Maple:
| > | cos(arctan(x)); |
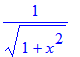
De opgaven 63 (a) en (b), 64 (a) en 66 (b) van § 1.6 leveren ook geen probleem op:
| > | arcsin(sqrt(3)/2); |
![]()
| > | arccos(-1); |
![]()
| > | arctan(-1); |
![]()
| > | arcsin(1); |
![]()
Ook de opgaven 67 (a) en (b) en 68 (a) gaan probleemloos:
| > | sin(arcsin(7/10)); |
![]()
| > | arctan(tan(4*Pi/3)); |
![]()
| > | sec(arctan(2)); |
![]()
Opgave 68 (b) levert meer problemen op:
| > | cos(2*arcsin(5/13)); |
![]()
Maar als we Maple een beetje helpen, dan lukt het wel. Er geldt: cos(2x)=1-2sin^2(x) . Dus:
| > | cos(2*arcsin(5/13))=1-2*(sin(arcsin(5/13)))^2; |
![]()
De opgaven 69 tot en met 71 gaan ook probleemloos:
| > | cos(arcsin(x)); |
![]()
| > | tan(arcsin(x)); |
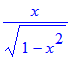
| > | sin(arctan(x)); |
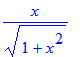
Opgave 72 lukt niet meteen:
| > | sin(2*arccos(x)); |
![]()
Maar als we Maple weer een beetje helpen, dan lukt het wel. Er geldt: sin(2x)=2sin(x)cos(x) . Dus:
| > | sin(2*arccos(x))=2*sin(arccos(x))*cos(arccos(x)); |
![]()
Kijk ook eens naar opgave 73:
| > | plot({sin(x),arcsin(x),x},x=-Pi/2..Pi/2); |
![[Maple Plot]](images/InverseTrigonometrischeFuncties19.gif)
Op het interval [-Pi/2,Pi/2] zijn de functies y=sin(x) en y=arcsin(x) elkaars inverse. De grafieken worden gespiegeld in de lijn y=x .
Opgave 76 is ook interessant:
| > | plot({sin(arcsin(x)),arcsin(sin(x))},x); |
![[Maple Plot]](images/InverseTrigonometrischeFuncties20.gif)
Wat is er aan de hand?
| > | sin(arcsin(x)); |
![]()
| > | arcsin(sin(x)); |
![]()
Voor alle x waarvoor arcsin(x) bestaat, dat wil zeggen voor -1<=x<=1 , geldt: -Pi/2<=arcsin(x)<=Pi/2 . Dan is dus: sin(arcsin(x))=x . Maple geeft echter ook voor x buiten het interval [-1,1] de waarde x .
sin(x) bestaat weliswaar voor alle waarden van x , maar arcsin(sin(x)) is alleen gelijk aan x op het interval -Pi/2<=x<=Pi/2 .
Bijvoorbeeld:
| > | arcsin(sin(3*Pi/2)); |
![]()
In § 3.6 van Stewart worden de afgeleiden van de inverse trigonometrische functies afgeleid:
| > | diff(arcsin(x),x);diff(arccos(x),x);diff(arctan(x),x); |
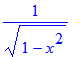
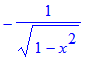
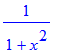
Let op het verschil met:
| > | D(arcsin);D(arccos);D(arctan); |
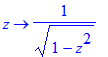
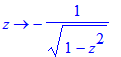
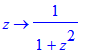
Deze laatste commando's leveren functies op met het voordeel dat je bijvoorbeeld een functiewaarde gemakkelijk kunt bepalen:
| > | D(arcsin)(1/2); |
![]()
Dit zou ook kunnen door de expressie arcsin(x) te differentiëren naar x en vervolgens voor x de waarde 1/2 te substitueren:
| > | diff(arcsin(x),x); |
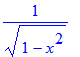
| > | subs(x=1/2,%); |
![]()
Opgave 46 van § 3.6:
| > | diff(arctan(x-sqrt(1+x^2)),x); |
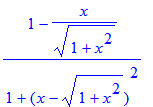
| > | simplify(%); |
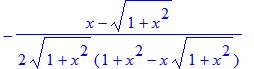
Toch kan dit nog verder worden vereenvoudigd tot 1/[2(1+x^2)] . Kijk maar:
| > | simplify(%-1/(2*(1+x^2))); |
![]()
Dit betekent dus dat de functie f(x)=arctan(x)-2arctan(x-sqrt(1+x^2)) constant is (de afgeleide is immers nul):
| > | f:=x->arctan(x)-2*arctan(x-sqrt(1+x^2)); |
![]()
| > | diff(f(x),x); |
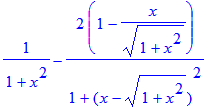
| > | simplify(%); |
![]()
| > | f(0); |
![]()
Blijkbaar geldt: arctan(x)-2arctan(x-sqrt(1+x^2))=Pi/2 voor alle x . Dit wordt geïllustreerd door de volgende grafiek:
| > | plot(f(x),x); |
![[Maple Plot]](images/InverseTrigonometrischeFuncties40.gif)
| > |