Meervoudige Integralen

>    restart:

Z ie: Stewart, hoofdstuk 15. Een meervoudige integraal moet in Maple worden ingevoerd als een herhaalde  integraal.

 Voorbeeld 1 van §  15.2:

>    Int(Int(x^2*y,y=1..2),x=0..3)=int(int(x^2*y,y=1..2),x=0..3);

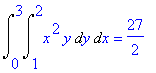
Int(Int(x^2*y,y = 1 .. 2),x = 0 .. 3) = 27/2

of

>    Int(Int(x^2*y,x=0..3),y=1..2)=int(int(x^2*y,x=0..3),y=1..2);

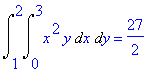
Int(Int(x^2*y,x = 0 .. 3),y = 1 .. 2) = 27/2

Voorbeeld 3 van §  15.2:

>    Int(Int(y*sin(x*y),x=1..2),y=0..Pi)=int(int(y*sin(x*y),x=1..2),y=0..Pi);

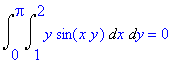
Int(Int(y*sin(x*y),x = 1 .. 2),y = 0 .. Pi) = 0

>    Int(Int(y*sin(x*y),y=0..Pi),x=1..2)=int(int(y*sin(x*y),y=0..Pi),x=1..2);

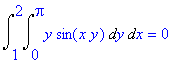
Int(Int(y*sin(x*y),y = 0 .. Pi),x = 1 .. 2) = 0

Voor Maple maakt het kennelijk niet zoveel uit in welke volgorde deze herhaalde integraal wordt uitgerekend. Dit gaat echter niet altijd op (zie: Stewart, § 15.3, voorbeeld 5):

>    Int(Int(sin(y^2),x=0..y),y=0..1)=int(int(sin(y^2),x=0..y),y=0..1);

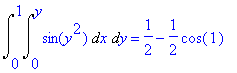
Int(Int(sin(y^2),x = 0 .. y),y = 0 .. 1) = 1/2-1/2*cos(1)

De andere volgorde levert aanzienlijk meer problemen op:

>    Int(Int(sin(y^2),y=x..1),x=0..1)=int(int(sin(y^2),y=x..1),x=0..1);

Int(Int(sin(y^2),y = x .. 1),x = 0 .. 1) = -1/12*hypergeom([3/4, 1],[3/2, 7/4, 2],-1/4)+1/2*FresnelS(2^(1/2)/Pi^(1/2))*2^(1/2)*Pi^(1/2)

Maple vindt weliswaar een antwoord in termen van allerlei Speciale Functies, maar het lijkt toch raadzaam om een handige volgorde te kiezen. Dat bovenstaande resultaten overeenkomen kan aannemelijk worden gemaakt door:

>    evalf(rhs(%));

>    evalf((1-cos(1))/2);

.2298488466

.2298488470

Stewart, §  15.3, opgave 48:

>    int(int(exp(x^4),x=y^(1/3)..2),y=0..8);

int(int(exp(x^4),x = y^(1/3) .. 2),y = 0 .. 8)

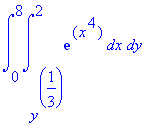
Hier laat Maple het blijkbaar afweten. In de andere volgorde lukt het wel:

>    Int(Int(exp(x^4),y=0..x^3),x=0..2)=int(int(exp(x^4),y=0..x^3),x=0..2);

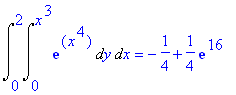
Int(Int(exp(x^4),y = 0 .. x^3),x = 0 .. 2) = -1/4+1/4*exp(16)

Dat het wel over dezelfde meervoudige integraal gaat wordt aannemelijk gemaakt door:

>    evalf(rhs(%));

>    evalf(int(int(exp(x^4),x=y^(1/3)..2),y=0..8));

2221527.380

2221527.380

Stewart, §  15.4, voorbeeld 3:

>    int(int(r,r=0..cos(2*theta)),theta=-Pi/4..Pi/4);

1/8*Pi

Dat het hier over poolcoördinaten gaat speelt eigenlijk geen rol; het is gewoon een herhaalde integraal. Maple gaat niet op eigen initiatief over op poolcoördinaten zoals blijkt uit opgave 29 van   §  15.4:

>    Int(Int(exp(x^2+y^2),y=0..sqrt(1-x^2)),x=0..1)=int(int(exp(x^2+y^2),y=0..sqrt(1-x^2)),x=0..1);

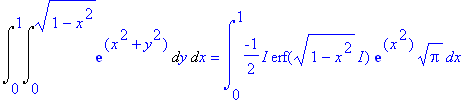
Int(Int(exp(x^2+y^2),y = 0 .. (1-x^2)^(1/2)),x = 0 .. 1) = int(-1/2*I*erf((1-x^2)^(1/2)*I)*exp(x^2)*Pi^(1/2),x = 0 .. 1)

We zullen Maple moeten vertellen dat er poolcoördinaten gebruikt moeten worden:

>    Int(Int(exp(x^2+y^2),y=0..sqrt(1-x^2)),x=0..1)=int(int(exp(r^2)*r,r=0..1),theta=0..Pi/2);

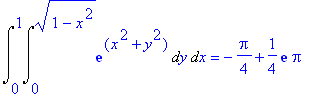
Int(Int(exp(x^2+y^2),y = 0 .. (1-x^2)^(1/2)),x = 0 .. 1) = -1/4*Pi+1/4*exp(1)*Pi

Drievoudige integralen gaan uiteraard op dezelfde manier. Zie: Stewart, § 15.7, voorbeeld 2:

>    int(int(int(z,z=0..1-x-y),y=0..1-x),x=0..1);

1/24

Voorbeeld 3 van § 15.7 ( E  opgevat als een gebied van type 3):

>    Int1:=int(int(int(sqrt(x^2+z^2),y=x^2+z^2..4),z=-sqrt(4-x^2)..sqrt(4-x^2)),x=-2..2);

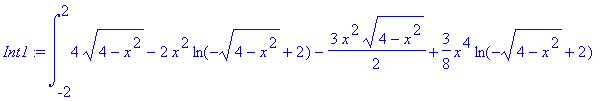
Int1 := int(4*(4-x^2)^(1/2)-2*x^2*ln(-(4-x^2)^(1/2)+2)-3/2*x^2*(4-x^2)^(1/2)+3/8*x^4*ln(-(4-x^2)^(1/2)+2)+2*x^2*ln((4-x^2)^(1/2)+2)-3/8*x^4*ln((4-x^2)^(1/2)+2),x = -2 .. 2)
Int1 := int(4*(4-x^2)^(1/2)-2*x^2*ln(-(4-x^2)^(1/2)+2)-3/2*x^2*(4-x^2)^(1/2)+3/8*x^4*ln(-(4-x^2)^(1/2)+2)+2*x^2*ln((4-x^2)^(1/2)+2)-3/8*x^4*ln((4-x^2)^(1/2)+2),x = -2 .. 2)

Laten we nu Maple maar vertellen hoe het beter kan (met poolco ö rdinaten):

>    Int2:=int(int((4-r^2)*r^2,r=0..2),theta=0..2*Pi);

Int2 := 128/15*Pi

Merk op dat we hiervoor eerst de drievoudige integraal moeten reduceren tot een tweevoudige integraal. Vervolgens moeten we de tweevoudige integraal schrijven in termen van poolco ö rdinaten.

Dat het hier weer steeds gaat over dezelfde drievoudige integraal kan weer aannemelijk worden gemaakt door:

>    evalf(Int1);

>    evalf(Int2);

26.80825731

26.80825731

Stewart, § 15.8, voorbeeld 2 (in Cartesische coördinaten):

>    Int1:=int(int(int(x^2+y^2,z=sqrt(x^2+y^2)..2),y=-sqrt(4-x^2)..sqrt(4-x^2)),x=-2..2);

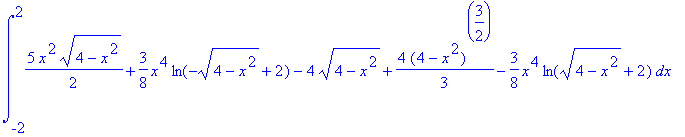
Int1 := int(5/2*x^2*(4-x^2)^(1/2)+3/8*x^4*ln(-(4-x^2)^(1/2)+2)-4*(4-x^2)^(1/2)+4/3*(4-x^2)^(3/2)-3/8*x^4*ln((4-x^2)^(1/2)+2),x = -2 .. 2)
Int1 := int(5/2*x^2*(4-x^2)^(1/2)+3/8*x^4*ln(-(4-x^2)^(1/2)+2)-4*(4-x^2)^(1/2)+4/3*(4-x^2)^(3/2)-3/8*x^4*ln((4-x^2)^(1/2)+2),x = -2 .. 2)

Nu met cilindercoördinaten:

>    Int2:=int(int(int(r^3,z=r..2),r=0..2),theta=0..2*Pi);

Int2 := 16/5*Pi

Ter controle:

>    evalf(Int1);

>    evalf(Int2);

10.05309649

10.05309649

Het volume van een bol met straal R  is (in Cartesische coördinaten):

>    Int(Int(Int(1,z=-sqrt(R^2-x^2-y^2)..sqrt(R^2-x^2-y^2)),y=-sqrt(R^2-x^2)..sqrt(R^2-x^2)),x=-R..R)=int(int(int(1,z=-sqrt(R^2-x^2-y^2)..sqrt(R^2-x^2-y^2)),y=-sqrt(R^2-x^2)..sqrt(R^2-x^2)),x=-R..R);

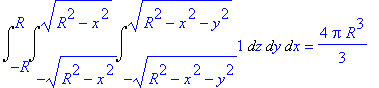
Int(Int(Int(1,z = -(R^2-x^2-y^2)^(1/2) .. (R^2-x^2-y^2)^(1/2)),y = -(R^2-x^2)^(1/2) .. (R^2-x^2)^(1/2)),x = -R .. R) = 4/3*Pi*R^3

Met behulp van bolcoördinaten:

>    Int(Int(Int(rho^2*sin(phi),rho=0..R),phi=0..Pi),theta=0..2*Pi)=int(int(int(rho^2*sin(phi),rho=0..R),phi=0..Pi),theta=0..2*Pi);

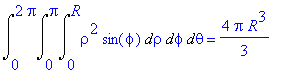
Int(Int(Int(rho^2*sin(phi),rho = 0 .. R),phi = 0 .. Pi),theta = 0 .. 2*Pi) = 4/3*Pi*R^3

Tenslotte kijken we nog even naar opgave 29 van § 15.8:

Met behulp van cilindercoördinaten vinden we voor het volume:

>    int(int(int(r,z=r..sqrt(1-r^2)),r=0..1/2*sqrt(2)),theta=0..2*Pi);

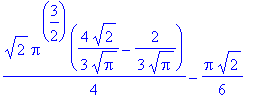
1/4*2^(1/2)*Pi^(3/2)*(4/3*2^(1/2)/Pi^(1/2)-2/3/Pi^(1/2))-1/6*Pi*2^(1/2)

oftewel

>    simplify(%);

1/3*2^(1/2)*Pi*(2^(1/2)-1)

En met behulp van bolcoördinaten:

>    m:=int(int(int(rho^2*sin(phi),rho=0..1),phi=0..Pi/4),theta=0..2*Pi);

m := 2/3*Pi-1/3*Pi*2^(1/2)

Voor het moment M   ten opzichte van het vlak z=0   vinden we met behulp van cilindercoördinaten:

>    int(int(int(z*r,z=r..sqrt(1-r^2)),r=0..1/2*sqrt(2)),theta=0..2*Pi);

1/8*Pi

en met behulp van bolcoö rdinaten:

>    M:=int(int(int(rho^3*cos(phi)*sin(phi),rho=0..1),phi=0..Pi/4),theta=0..2*Pi);

M := 1/8*Pi

Voor de z -coördinaat van het zwaartepunt (of massamiddelpunt) vinden we dus in beide gevallen:

>    simplify(M/m);

-3/8/(-2+2^(1/2))

>