Oneigenlijke Integralen

Oneigenlijke integralen

> restart:

Z ie: Stewart, § 7.8. Maple kan ook goed overweg met oneigenlijke integralen van de eerste soort:

> Int(1/x,x=1..infinity)=int(1/x,x=1..infinity);

> Int(x*exp(x),x=-infinity..0)=int(x*exp(x),x=-infinity..0);

> Int(1/(1+x^2),x=-infinity..infinity)=int(1/(1+x^2),x=-infinity..infinity);

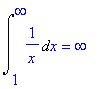
Int(1/x,x = 1 .. infinity) = infinity

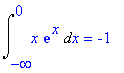
Int(x*exp(x),x = -infinity .. 0) = -1

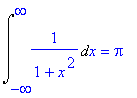
Int(1/(1+x^2),x = -infinity .. infinity) = Pi

Dit zijn de eerste drie voorbeelden van § 7.8.

Nu voorbeeld 4 :

> Int(1/(x^p),x=1..infinity)=int(1/(x^p),x=1..infinity);

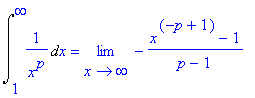
Int(1/(x^p),x = 1 .. infinity) = limit(-(x^(-p+1)-1)/(p-1),x = infinity)

Voor is dit correct. Voor p>1, p<1 en p=1 vinden we dan achtereenvolgens:

> assume(p>1);Int(1/(x^p),x=1..infinity)=int(1/(x^p),x=1..infinity);

> assume(p<1);Int(1/(x^p),x=1..infinity)=int(1/(x^p),x=1..infinity);

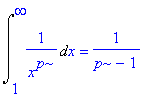
Int(1/(x^p),x = 1 .. infinity) = 1/(p-1)

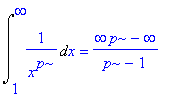
Int(1/(x^p),x = 1 .. infinity) = (infinity*p-infinity)/(p-1)

Zo gaat het beter:

> Limit((1-x^(-p+1))/(p-1),x=infinity)=limit((1-x^(-p+1))/(p-1),x=infinity);

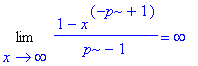
Limit((1-x^(-p+1))/(p-1),x = infinity) = infinity

En ten slotte:

> assume(p=1);Int(1/(x^p),x=1..infinity)=int(1/(x^p),x=1..infinity);

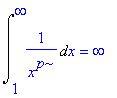
Int(1/(x^p),x = 1 .. infinity) = infinity

Oneigenlijke integralen van de tweede soort:

> Int(1/sqrt(x-2),x=2..5)=int(1/sqrt(x-2),x=2..5);

> Int(sec(x),x=0..Pi/2)=int(sec(x),x=0..Pi/2);

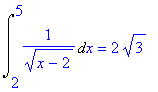
Int(1/((x-2)^(1/2)),x = 2 .. 5) = 2*3^(1/2)

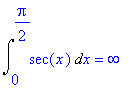
Int(sec(x),x = 0 .. 1/2*Pi) = infinity

Dit zijn de voorbeelden 5 en 6.

Dan voorbeeld 7:

> Int(1/(x-1),x=0..3)=int(1/(x-1),x=0..3);

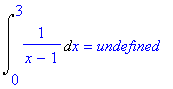
Int(1/(x-1),x = 0 .. 3) = undefined

Net als in het boek brengen we nu een splitsing aan:

> Int(1/(x-1),x=0..1)=int(1/(x-1),x=0..1);

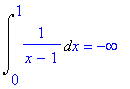
Int(1/(x-1),x = 0 .. 1) = -infinity

Voorbeeld 8:

> Int(ln(x),x=0..1)=int(ln(x),x=0..1);

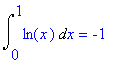
Int(ln(x),x = 0 .. 1) = -1

Maple kan zelfs de voorbeelden 9 en 10 aan:

> Int(exp(-x^2),x=0..infinity)=int(exp(-x^2),x=0..infinity);

> Int((1+exp(-x))/x,x=1..infinity)=int((1+exp(-x))/x,x=1..infinity);

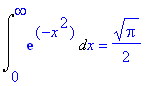
Int(exp(-x^2),x = 0 .. infinity) = 1/2*Pi^(1/2)

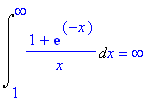
Int((1+exp(-x))/x,x = 1 .. infinity) = infinity

Maar kijken we bijvoorbeeld naar opgave 52 van § 7.8 dan wordt het lastiger:

> Int(x/sqrt(1+x^6),x=1..infinity)=int(x/sqrt(1+x^6),x=1..infinity);

Int(x/(1+x^6)^(1/2),x = 1 .. infinity) = hypergeom([1/6, 1/2],[7/6],-1)

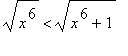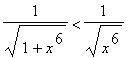Maple geeft het resultaat in de vorm van een hypergeometrische functie. Blijkbaar is de integraal convergent. Dit kunnen we alsvolgt inzien. Er geldt: sqrt(x^6) < sqrt(x^6+1) en dus 1/sqrt(1+x^6) < 1/sqrt(x^6) .

De integraal is dus kleiner dan:

> Int(x/sqrt(0+x^6),x=1..infinity)=int(x/sqrt(0+x^6),x=1..infinity);

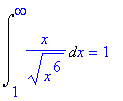
Int(x/(x^6)^(1/2),x = 1 .. infinity) = 1

Maple kan de integraal overigens ook benaderen:

> evalf(int(x/sqrt(1+x^6),x=1..infinity));

>