![[Maple Plot]](images/PartieleAfgeleiden1.gif)
Partiėle afgeleiden
| > | restart: |
Zi e: Stewart, § 14.1 - § 14.4. We beginnen met het laden van het pakket plots :
| > | with(plots): |
De grafieken in figuur 10 van § 14.1 van Stewart kunnen alsvolgt worden geproduceerd:
| > | plot3d((x^2+3*y^2)*exp(-x^2-y^2),x=-3..3,y=-3..3); |
![[Maple Plot]](images/PartieleAfgeleiden1.gif)
| > | plot3d((x^2+3*y^2)*exp(-x^2-y^2),x=-3..3,y=-3..3,orientation=[145,120]); |
![[Maple Plot]](images/PartieleAfgeleiden2.gif)
| > | plot3d(sin(x)+sin(y),x=-5..5,y=-5..5); |
![[Maple Plot]](images/PartieleAfgeleiden3.gif)
| > | plot3d(sin(x)*sin(y)/(x*y),x=-10..10,y=-10..10); |
![[Maple Plot]](images/PartieleAfgeleiden4.gif)
In voorbeeld 11 van § 14.1 worden de
niveaukrommen
van de functie
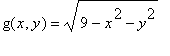 bepaald resulterend in de
contour map
in figuur 16. In Maple kan dit worden gedaan met behulp van het commando
contourplot
:
bepaald resulterend in de
contour map
in figuur 16. In Maple kan dit worden gedaan met behulp van het commando
contourplot
:
| > | contourplot(sqrt(9-x^2-y^2),x=-4..4,y=-4..4); |
![[Maple Plot]](images/PartieleAfgeleiden6.gif)
We kunnen echter ook gebruikmaken van het commando implicitplot alsvolgt:
| > | implicitplot({seq(x^2+y^2=9-k^2,k=0..3)},x=-4..4,y=-4..4,numpoints=10000); |
![[Maple Plot]](images/PartieleAfgeleiden7.gif)
Als we nu proberen deze niveaukrommen op hoogte voor te stellen zodat ze een oppervlak vormen, dan krijgen we:
| > | plot3d(sqrt(9-x^2-y^2),x=-4..4,y=-4..4,filledregions=true,style=contour); |
![[Maple Plot]](images/PartieleAfgeleiden8.gif)
De grafiek van de functie in figuur 7 is:
| > | plot3d(sqrt(9-x^2-y^2),x=-4..4,y=-4..4); |
![[Maple Plot]](images/PartieleAfgeleiden9.gif)
Een functie
![]() van twee variabelen
van twee variabelen
![]() en
en
![]() kan alsvolgt worden gedefinieerd:
kan alsvolgt worden gedefinieerd:
| > | f := (x,y) -> -x*y*exp(-x^2-y^2); |
![]()
Vergelijk met figuur 19 van § 14.1:
| > | contourplot(f(x,y),x=-2..2,y=-2..2); |
![[Maple Plot]](images/PartieleAfgeleiden14.gif)
| > | plot3d(f(x,y),x=-2..2,y=-2..2); |
![[Maple Plot]](images/PartieleAfgeleiden15.gif)
De
eerste partiėle afgeleiden
van
![]() zijn:
zijn:
| > | diff(f(x,y),x); diff(f(x,y),y); |
![]()
![]()
Hier hebben we de expressie
![]() respectievelijk gedifferentieerd naar de variabelen
respectievelijk gedifferentieerd naar de variabelen
![]() en
en
![]() .
.
Als functies worden deze genoteerd als:
| > | D[1](f); D[2](f); |
![]()
![]()
Kijk nu eens naar voorbeeld 3 van § 14.3:
| > | f := (x,y) -> sin(x/(1+y)); |
![]()
De eerste partiėle afgeleiden zijn:
| > | D[1](f); D[2](f); |
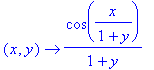
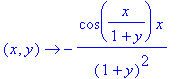
Voorbeeld 4 van § 14.3:
| > | eq:=x^3+y^3+z^3+6*x*y*z=1; |
![]()
Figuur 6:
| > | implicitplot3d(eq,x=-2..2,y=-2..2,z=-2..2); |
![[Maple Plot]](images/PartieleAfgeleiden28.gif)
De
eerste partiėle afgeleiden
van
![]() naar de variabelen
naar de variabelen
![]() en
en
![]() zijn respectievelijk:
zijn respectievelijk:
| > | implicitdiff(eq,z,x); |
| > | implicitdiff(eq,z,y); |
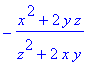
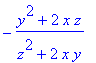
Voorbeeld 6 van § 14.3:
| > | f := (x,y) -> x^3+x^2*y^3-2*y^2; |
![]()
De eerste partiėle afgeleiden zijn:
| > | D[1](f); D[2](f); |
![]()
![]()
De tweede partiėle afgeleiden zijn:
| > | D[1,1](f); D[1,2](f); D[2,1](f); D[2,2](f); |
![]()
![]()
![]()
![]()
Differentiėren we de expressie
![]() dan krijgen we:
dan krijgen we:
| > | diff(f(x,y),x$2); diff(diff(f(x,y),x),y); diff(diff(f(x,y),x),y); diff(f(x,y),y$2); |
![]()
![]()
![]()
![]()
Voorbeeld 7 van § 14.3:
| > | f := (x,y,z) -> sin(3*x+y*z); |
![]()
| > | D[1,1,2,3](f); |
![]()
| > | diff(diff(diff(f(x,y,z),x$2),y),z); |
![]()
De
stelling van Clairaut
in
§ 14.3 stelt dat de gemengde tweede partiėle afgeleiden van een functie
![]() gelijk zijn in een punt (a,b) als beide functies continu zijn op een cirkelschijfje rond dat punt (a,b).
gelijk zijn in een punt (a,b) als beide functies continu zijn op een cirkelschijfje rond dat punt (a,b).
Blijkbaar neemt Maple aan dat dit altijd geldt:
| > | restart: D[1,2](f)-D[2,1](f); |
![]()
Voorbeeld 8 van § 14.3:
| > | u := (x,y) -> exp(x)*sin(y); |
![]()
| > | diff(u(x,y),x$2)+diff(u(x,y),y$2); |
![]()
Voorbeeld 9 van § 14.3:
| > | u := (x,t) -> sin(x-a*t); |
![]()
| > | diff(u(x,t),t$2)-a^2*diff(u(x,t),x$2); |
![]()
Voorbeeld 1 van § 14.4:
| > | f := (x,y) -> 2*x^2+y^2; |
![]()
Het
raakvlak
aan de grafiek van
![]() in het punt (1,1,3) is:
in het punt (1,1,3) is:
| > | z = f(1,1)+D[1](f)(1,1)*(x-1)+D[2](f)(1,1)*(y-1); |
![]()
Figuur 2 kan nu alsvolgt worden geproduceerd:
| > | with(plots): plot3d({2*x^2+y^2,4*x+2*y-3},x=-4..4,y=-4..4); |
![[Maple Plot]](images/PartieleAfgeleiden58.gif)
| > |