Taylorreeksen
| > | restart: |
Z ie: Stewart, hoofdstuk 11. Maple kan de Taylorreeks van een functie bepalen, zoals bijvoorbeeld:
| > | taylor(exp(x),x=0); |
![]()
Standaard geeft Maple de uitkomst tot de orde:
| > | Order; |
![]()
Dit kunnen we eventueel aanpassen door de orde expliciet aan te geven:
| > | taylor(exp(x),x=0,10); |
![]()
Of door eerst de waarde van Order te wijzigen:
| > | Order:=12: taylor(exp(x),x=0); |
![]()
We zetten Order weer terug op de standaardwaarde en proberen eens een Taylorreeks rond x=1 :
| > | Order:=6: taylor(exp(x),x=1); |
![]()
Met behulp van Maple kunnen we nu eenvoudig de Taylorreeksen van het formuleblad (zie ook: Stewart, § 11.10) controleren:
| > | exp(x)=taylor(exp(x),x=0,4); |
| > | sin(x)=taylor(sin(x),x=0,8); |
| > | cos(x)=taylor(cos(x),x=0,8); |
| > | ln(1+x)=taylor(ln(1+x),x=0,5); |
| > | (1+x)^k=taylor((1+x)^k,x=0,4); |
![]()
![]()
![]()
![]()
![]()
Voorbeeld 6 van § 11.10:
| > | taylor(x*cos(x),x=0); |
![]()
Voorbeeld 7 van § 11.10:
| > | taylor(sin(x),x=Pi/3); |
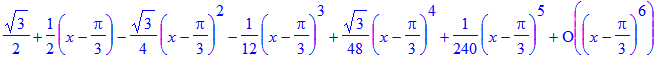
Nog enkele voorbeelden (zie: Stewart, § 11.10):
| > | 1/(1-x)=taylor(1/(1-x),x=0); |
| > | arctan(x)=taylor(arctan(x),x=0); |
| > | exp(x)*sin(x)=taylor(exp(x)*sin(x),x=0); |
| > | tan(x)=taylor(tan(x),x=0); |
![]()
![]()
![]()
![]()
Voorbeeld 1 van § 11.11:
| > | 1/(1+x)^2=taylor(1/(1+x)^2,x=0); |
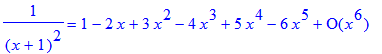
Dit is een voorbeeld van een binomiaalreeks , waarbij de volgende binomiaalcoëfficiënten optreden:
| > | for n from 0 to 5 do binomial(-2,n) od; |
![]()
![]()
![]()
![]()
![]()
![]()
Voorbeeld 2 van § 11.11:
| > | 1/sqrt(4-x)=taylor(1/sqrt(4-x),x=0); |
![]()
Schrijven we
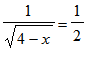 *
*
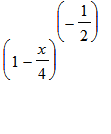 , dan vinden we dus:
, dan vinden we dus:
| > | 1/sqrt(4-x)=1/2*taylor((1-x/4)^(-1/2),x=0); |
![]()
Hierin treden de volgende binomiaalcoëfficiënten op:
| > | for n from 0 to 5 do binomial(-1/2,n) od; |
![]()
![]()
![]()
![]()
![]()
![]()
| > |