De rij van Fibonacci

De rij van Fibonacci is bekend bij Maple in het pakket combinat :

>    with(combinat):

Het commando fibonacci(n)  geeft nu het n-de getal uit de rij van Fibonacci:

F_{n+2}=F_n+F_{n+1} met F_1=F_2=1.

>    fibonacci(1);

1

>    fibonacci(2);

1

>    fibonacci(3);

2

De algemene formule is dan: F_n=[(1+sqrt(5))^n-(1-sqrt(5))^n]/(2^n*sqrt(5)), n=0,1,2,...

>    F:=n->simplify(((1+sqrt(5))^n-(1-sqrt(5))^n)/(2^n*sqrt(5)));

F := n -> simplify(((1+sqrt(5))^n-(1-sqrt(5))^n)/(2^n)/sqrt(5))

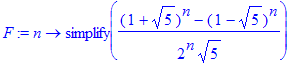
>    F(1);

1

>    F(2);

1

>    F(3);

2

Het 100ste getal uit de rij van Fibonacci is dus:

>    fibonacci(100);

354224848179261915075

>    F(100);

354224848179261915075

>