


Volgende: Over dit dokument ...
Omhoog: Construeerbare en niet-construeerbare punten
Vorige: Construeerbare en niet-construeerbare punten
We voeren coördinaten in: we vatten het punt 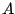 op als oorsprong.
De lijn door
op als oorsprong.
De lijn door 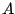 en
en 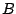 wordt de
wordt de  -as, op zo'n manier dat
-as, op zo'n manier dat 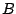 samen valt met
het punt
samen valt met
het punt 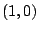 . Dus
. Dus 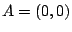 en
en 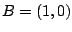 .
De cirkel met middelpunt
.
De cirkel met middelpunt 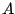 en straal
en straal 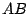 is nu de eenheidcirkel geworden,
en
is nu de eenheidcirkel geworden,
en 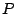 is het punt
is het punt
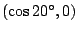 .
.
De formule
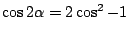 geeft
geeft
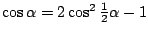 .
Hieruit volgt dat
.
Hieruit volgt dat
We kunnen hiermee formules voor
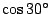 ,
,
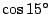 en
en
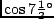 afleiden:
afleiden:
en
Deze formules illustreren twee belangrijke
feiten over construeerbare getallen die we (zonder bewijs)
zullen gebruiken.
A.
Alle construeerbare getallen ontstaan uit 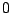 en
en 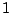 door optellen, aftrekken, vermenigvuldigen, delen en (vierkants)wortels te
trekken.
door optellen, aftrekken, vermenigvuldigen, delen en (vierkants)wortels te
trekken.
B.
Elk construeerbaar getal is oplossing van een vergelijking van de vorm
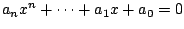 , waarbij de
, waarbij de 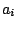 gehele getallen zijn.
De kleinst mogelijke
gehele getallen zijn.
De kleinst mogelijke 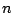 die we hier kunnen nemen, is een macht van
die we hier kunnen nemen, is een macht van 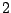 .
Zo is
.
Zo is
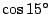 een oplossing van de
vergelijking
een oplossing van de
vergelijking
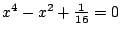 (kwadrateer links en rechts in
(kwadrateer links en rechts in
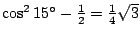 ).
Voor
).
Voor
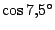 is zelfs een achtstegraads vergelijking
nodig. Probeer deze vergelijking maar eens op te schrijven.
is zelfs een achtstegraads vergelijking
nodig. Probeer deze vergelijking maar eens op te schrijven.
De somregel voor de cosinus luidt
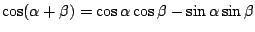 .
Deze regel kunnen we gebruiken om een formnule voor
.
Deze regel kunnen we gebruiken om een formnule voor 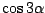 te vinden:
te vinden:
Vullen we in
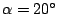 , dan vinden we
, dan vinden we
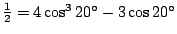 .
Vermenigvuldigen we deze vergelijking met 2,
dan vinden we dat
.
Vermenigvuldigen we deze vergelijking met 2,
dan vinden we dat
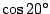 een oplossing is van de vergelijking
een oplossing is van de vergelijking
Dit is een derdegraads vergelijking.
Stel dat 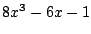 te ontbinden is.
Dan zijn er gehele
getallen
te ontbinden is.
Dan zijn er gehele
getallen 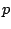 ,
, 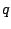 ,
, 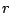 ,
, 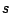 en
en 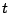 zó dat
zó dat
Hieruit volgt dat 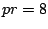 ,
, 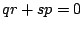 ,
, 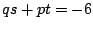 en
en 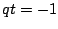 .
Het is nu een eenvoudige opgave om na te gaan dat
zulke
.
Het is nu een eenvoudige opgave om na te gaan dat
zulke 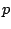 ,
, 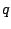 ,
, 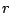 ,
, 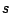 en
en 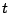 niet bestaan.
De vergelijking
niet bestaan.
De vergelijking 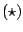 is dus niet te ontbinden
met behulp van gehele getallen.
De minimale graad van een vergelijking voor
is dus niet te ontbinden
met behulp van gehele getallen.
De minimale graad van een vergelijking voor
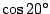 is daarom
gelijk aan
is daarom
gelijk aan 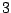 .
Dit is geen macht van
.
Dit is geen macht van 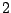 ,
en daarom is
,
en daarom is
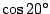 niet construeerbaar.
niet construeerbaar.



Volgende: Over dit dokument ...
Omhoog: Construeerbare en niet-construeerbare punten
Vorige: Construeerbare en niet-construeerbare punten
KP Hart
2004-12-23
![]() op als oorsprong.
De lijn door
op als oorsprong.
De lijn door ![]() en
en ![]() wordt de
wordt de ![]() -as, op zo'n manier dat
-as, op zo'n manier dat ![]() samen valt met
het punt
samen valt met
het punt ![]() . Dus
. Dus ![]() en
en ![]() .
De cirkel met middelpunt
.
De cirkel met middelpunt ![]() en straal
en straal ![]() is nu de eenheidcirkel geworden,
en
is nu de eenheidcirkel geworden,
en ![]() is het punt
is het punt
![]() .
.
![]() geeft
geeft
![]() .
Hieruit volgt dat
.
Hieruit volgt dat
![]() .
Deze regel kunnen we gebruiken om een formnule voor
.
Deze regel kunnen we gebruiken om een formnule voor ![]() te vinden:
te vinden: