We kunnen constructies afzonderlijk bekijken,
maar we kunnen ook systematisch nagaan welke punten
we krijgen als we beginnen met twee punten ![]() en
en ![]() .
We kunnen om te beginnen de lijn door
.
We kunnen om te beginnen de lijn door ![]() en
en ![]() trekken en de cirkels om
trekken en de cirkels om ![]() en
en ![]() met straal
met straal ![]() .
.

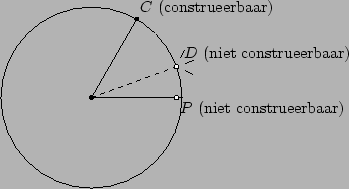
Het antwoord op deze vraag is: ``Neen''. Om dit te bewijzen
is het voldoende een voorbeeld te geven van een
punt dat niet te construeren is.
Wij geven zo'n punt.
Trek een cirkel met middelpunt ![]() en straal
en straal ![]() .
Kies op deze cirkel een punt
.
Kies op deze cirkel een punt ![]() zodat
zodat
![]() .
Projecteer dit punt loodrecht op het lijnstuk
.
Projecteer dit punt loodrecht op het lijnstuk ![]() , noem de projectie
, noem de projectie ![]() .
Het punt
.
Het punt ![]() is ons voorbeeld: je kunt het punt wel tekenen met je geodriehoek,
maar je kunt het niet construeren met alleen passer en liniaal.
Dit betekent ook dat je niet elke hoek
met passer en liniaal in drie gelijke hoeken kan delen.
Immers, op de cirkel kun je, uitgaande van alleen
is ons voorbeeld: je kunt het punt wel tekenen met je geodriehoek,
maar je kunt het niet construeren met alleen passer en liniaal.
Dit betekent ook dat je niet elke hoek
met passer en liniaal in drie gelijke hoeken kan delen.
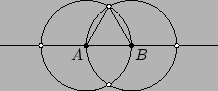
Immers, op de cirkel kun je, uitgaande van alleen ![]() en
en ![]() wèl een punt
wèl een punt ![]() construeren met
construeren met
![]() .
Als we deze hoek van
.
Als we deze hoek van ![]() met passer en liniaal in drieën
zouden kunnen delen, dan zouden we met passer en liniaal
met passer en liniaal in drieën
zouden kunnen delen, dan zouden we met passer en liniaal ![]() kunnen
construeren, en daarmee ook
de loodrechte projectie
kunnen
construeren, en daarmee ook
de loodrechte projectie ![]() op de
op de ![]() -as.
-as.