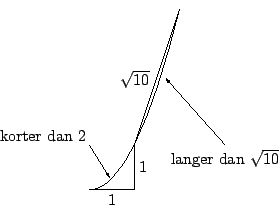Next: Wat is het wel?
Up: De Kettinglijn
Previous: De Kettinglijn
Dat het touw geen parabool beschrijft volgt uit een karakteristieke
eigenschap van de vorm van het touw en een karakteristieke eigenschap
van de parabool.
Eerst het touw:
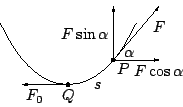
we nemen een punt 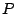 ergens op het touw en bekijken de kracht
ergens op het touw en bekijken de kracht 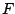 die
naar rechtsboven trekt.
De horizontale component van die kracht is gelijk aan de horizontale
kracht
die
naar rechtsboven trekt.
De horizontale component van die kracht is gelijk aan de horizontale
kracht 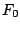 die in het laagste punt
die in het laagste punt 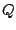 naar links trekt -- omdat het touw
niet beweegt wordt er blijkbaar in
naar links trekt -- omdat het touw
niet beweegt wordt er blijkbaar in 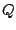 en
en 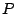 even hard getrokken.
Dit geeft de vergelijking
even hard getrokken.
Dit geeft de vergelijking
Vertikaal moet de kracht het stuk touw tussen 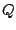 en
en 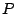 ophouden
en dat vergt
ophouden
en dat vergt 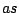 ; hierin is
; hierin is 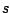 de lengte van het stuk touw
en
de lengte van het stuk touw
en 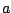 een constante waar de soortelijke massa en de zwaartekracht in verwerkt
zijn.
We krijgen dus als tweede vergelijking:
een constante waar de soortelijke massa en de zwaartekracht in verwerkt
zijn.
We krijgen dus als tweede vergelijking:
Als we deze vergelijkingen op elkaar delen krijgen we
waarbij we 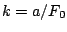 stellen.
Wat dit betekent is dat de helling van de raaklijn in een punt aan de kromme
recht evenredig is met de lengte van het stuk tussen dat punt en het laagste
punt.
stellen.
Wat dit betekent is dat de helling van de raaklijn in een punt aan de kromme
recht evenredig is met de lengte van het stuk tussen dat punt en het laagste
punt.
Nu kijken we naar een parabool van de vorm 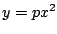 .
.
In een punt 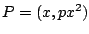 op de parabool is de helling van de raaklijn
gelijk aan
op de parabool is de helling van de raaklijn
gelijk aan 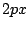 , met andere woorden
, met andere woorden
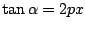 .
.
Als ons touw een parabool zou beschrijven dan zou in elk punt
de betrekking
moeten gelden; met andere woorden: de booglengte is recht evenredig
met de 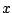 -coördinaat.
In het bijzonder zouden de booglengten van
-coördinaat.
In het bijzonder zouden de booglengten van 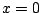 tot
tot 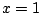 en die van
en die van 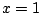 tot
tot 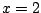 even lang moeten zijn.
Maar voor de parabool
even lang moeten zijn.
Maar voor de parabool 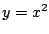 kan dat duidelijk niet:
het eerste stuk is korter dan
kan dat duidelijk niet:
het eerste stuk is korter dan 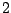 ; het tweede stuk is langer dan
; het tweede stuk is langer dan 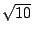 .
.
Je kunt zelfs bewijzen dat een kromme waarvan de booglengte recht evenredig
is met de 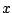 -coördinaat een rechte lijn moet zijn.
-coördinaat een rechte lijn moet zijn.



Next: Wat is het wel?
Up: De Kettinglijn
Previous: De Kettinglijn
KP Hart
2006-04-06

![]() .
.