


Volgende: De logaritmische spiraal
Omhoog: Spiralen
Vorige: Spiralen
De spiraal van Archimedes heeft als vergelijking 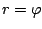 . Dit betekent dat we een lijn om de oorsprong laten draaien en telkens, als die lijn de hoek
. Dit betekent dat we een lijn om de oorsprong laten draaien en telkens, als die lijn de hoek 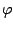 (in radialen) met de
(in radialen) met de 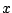 -as maakt op die lijn het punt met afstand
-as maakt op die lijn het punt met afstand 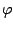 tot de oorsprong nemen. Als de lijn eenmaal rond is geweest gaan we gewoon door, we laten
tot de oorsprong nemen. Als de lijn eenmaal rond is geweest gaan we gewoon door, we laten 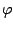 alle waarden van
alle waarden van 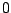 tot
tot 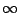 aannemen. We krijgen dan het plaatje in figuur 1.
aannemen. We krijgen dan het plaatje in figuur 1.
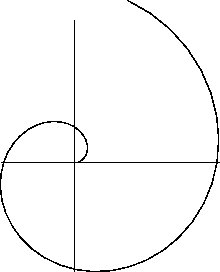
Figuur 1:
Spiraal van Archimedes
 |
Je kunt hierop variëren door andere machten van 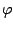 te nemen; bekende spiralen zijn die van Fermat (
te nemen; bekende spiralen zijn die van Fermat (
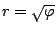 ), de hyperbolische spiraal (
), de hyperbolische spiraal (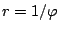 ) en de Lituus (
) en de Lituus (
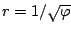 ). Als je de Lituus probeert te tekenen zie je waar de naam vandaan komt: 'lituus' is de naam van een staf waar de staf van Sinterklaas van afgeleid is.
). Als je de Lituus probeert te tekenen zie je waar de naam vandaan komt: 'lituus' is de naam van een staf waar de staf van Sinterklaas van afgeleid is.
KP Hart
2006-04-12

![]() te nemen; bekende spiralen zijn die van Fermat (
te nemen; bekende spiralen zijn die van Fermat (
![]() ), de hyperbolische spiraal (
), de hyperbolische spiraal (![]() ) en de Lituus (
) en de Lituus (
![]() ). Als je de Lituus probeert te tekenen zie je waar de naam vandaan komt: 'lituus' is de naam van een staf waar de staf van Sinterklaas van afgeleid is.
). Als je de Lituus probeert te tekenen zie je waar de naam vandaan komt: 'lituus' is de naam van een staf waar de staf van Sinterklaas van afgeleid is.