De logaritmische spiraal

In 1638 ontdekte Descartes de logaritmische spiraal toen hij een kromme zocht die elke lijn door de oorsprong onder dezelfde hoek $\alpha$ snijdt. Het blijkt dat die kromme de vergelijking $r=e^{a\varphi}$ moet hebben, met $a=\cos\alpha/\sin\alpha$.

Figuur 2: De logaritmische spiraal $r=e^{\varphi /5}$

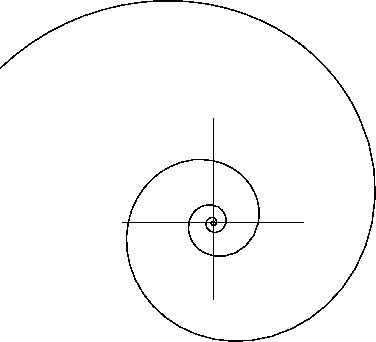
De wiskundige Jacob Bernoulli heeft deze kromme met behulp van de in zijn tijd gloednieuwe differentiaal- en integraalrekening nauwkeurig onderzocht. Zo kon hij de lengte van elk stuk van de spiraal uitrekenen. Als je bijvoorbeeld $\varphi$ van $0$ tot $2\pi$ laat toenemen (één omwenteling) dan is de lengte van het bijbehorende stuk precies ${1\over a}\sqrt{1+a^2}(e^{2a\pi}-1)$. De oneindig vele omwentelingen die je krijgt als $\varphi$ van $-\infty$ tot $0$ toeneemt blijken bij elkaar een eindige lengte hebben: ${1\over a}\sqrt{1+a^2}$.

De logaritmische spiraal is bijzonder goed bestand tegen transformaties. Als je alle punten in het vlak met dezelfde constante $k$ vermenigvuldigd, dan blijft de spiraal nagenoeg zichzelf: in plaats van $r=e^{a\varphi}$ krijg je $r=ke^{a\varphi}$. Hoewel het lijkt of de spiraal opgerekt wordt is dat maar schijn. Neem de logaritme van $k$ maar en deel die door $a$, dat wil zeggen $\theta={1\over a}\ln k$. Dan kunnen we schrijven $r=ke^{a\varphi}=e^{a(\varphi+\theta)}$. Hieruit blijkt dat de spiraal eigenlijk alleen maar gedraaid is over $-\theta$ radialen.