


Next: About this document ...
Up: Sinus en cosinus
Previous: Hoe kan dat nou?
Nu hebben we wel heel leuk uit een plaatje afgelezen dat
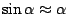 en daaruit afgeleid dat
en daaruit afgeleid dat
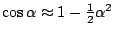 , maar we moeten natuurlijk wel controleren
hoe goed die benaderingen zijn.
Dat kunnen we met een beetje werk redelijk eenvoudig doen.
, maar we moeten natuurlijk wel controleren
hoe goed die benaderingen zijn.
Dat kunnen we met een beetje werk redelijk eenvoudig doen.
Om te beginnen geldt
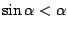 en daarmee vinden we meteen dat
en daarmee vinden we meteen dat
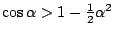 .
Uit het volgende plaatje kunnen we aflezen dat
.
Uit het volgende plaatje kunnen we aflezen dat
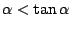 :
:
de taartpunt heet oppervlakte
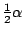 en de oppervlakte van de grote
driehoek is
en de oppervlakte van de grote
driehoek is
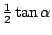 .
Hieruit volgt weer dat
.
Hieruit volgt weer dat
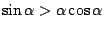 en met
en met
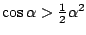 vinden we
vinden we
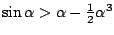 .
Conclusie
.
Conclusie
Dus, als we zeggen dat
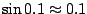 dan zitten we er op z'n hoogst
maar
dan zitten we er op z'n hoogst
maar 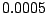 naast!
naast!
Nu kunnen we ook de benadering van 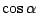 controleren via de
formule
controleren via de
formule
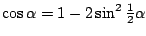 :
:
De rechterkant is gelijk aan
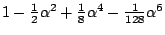 .
Conclusie
.
Conclusie
Hiermee kunnen we uitrekenen hoe erg ik er naast zat met mijn antwoord:
op z'n hoogst
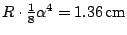 .
Dit valt in het niet tegen alle mogelijke afrondfouten die bij het
meten van de afstand Amsterdam-Groningen en het bepalen van de straal
van de aarde gemaakt worden.
Probeer de berekening nog maar eens met de afgeronde waarden
.
Dit valt in het niet tegen alle mogelijke afrondfouten die bij het
meten van de afstand Amsterdam-Groningen en het bepalen van de straal
van de aarde gemaakt worden.
Probeer de berekening nog maar eens met de afgeronde waarden
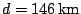 en
en
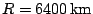 .
.



Next: About this document ...
Up: Sinus en cosinus
Previous: Hoe kan dat nou?
KP Hart
2004-03-05
![]() en daaruit afgeleid dat
en daaruit afgeleid dat
![]() , maar we moeten natuurlijk wel controleren
hoe goed die benaderingen zijn.
Dat kunnen we met een beetje werk redelijk eenvoudig doen.
, maar we moeten natuurlijk wel controleren
hoe goed die benaderingen zijn.
Dat kunnen we met een beetje werk redelijk eenvoudig doen.
![]() en daarmee vinden we meteen dat
en daarmee vinden we meteen dat
![]() .
Uit het volgende plaatje kunnen we aflezen dat
.
Uit het volgende plaatje kunnen we aflezen dat
![]() :
:
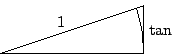
![]() controleren via de
formule
controleren via de
formule
![]() :
: