


Next: Een ongelijkheid
Up: augustus-1
Previous: augustus-1
Iedereen weet hoe je `het' gemiddelde van twee getallen 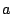 en
en 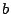 bepaalt:
optellen en delen door
bepaalt:
optellen en delen door 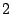 , het gemiddelde is
, het gemiddelde is 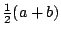 .
Dat dit gemiddelde niet altijd het juiste gemiddelde is blijkt uit het volgende
voorbeeld.
Je hebt een balans waarvan de armen niet even lang zijn.
Als een brief links hangt moet er rechts
.
Dat dit gemiddelde niet altijd het juiste gemiddelde is blijkt uit het volgende
voorbeeld.
Je hebt een balans waarvan de armen niet even lang zijn.
Als een brief links hangt moet er rechts 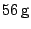 bij om de zaak in evenwicht
te krijgen; met de brief rechts hoeft er links maar
bij om de zaak in evenwicht
te krijgen; met de brief rechts hoeft er links maar 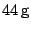 bij.
Hoe zwaar is de brief nu?
Je kunt dat uitrekenen met behulp van de wet
``
bij.
Hoe zwaar is de brief nu?
Je kunt dat uitrekenen met behulp van de wet
``
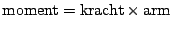 ''.
Als we het gewicht van de brief even
''.
Als we het gewicht van de brief even 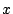 noemen (en de lengte van de
linker- en rechterarm respectievelijk
noemen (en de lengte van de
linker- en rechterarm respectievelijk 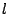 en
en 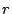 ) dan zegt de eerste
weging ons dat
) dan zegt de eerste
weging ons dat
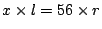 ; de tweede weging geeft
; de tweede weging geeft
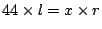 .
Hieruit volgt dan weer dat
.
Hieruit volgt dan weer dat 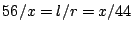 en dus
en dus
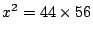 .
We zien dat de brief
.
We zien dat de brief
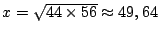 gram zwaar is; iets minder dan het gewone gemiddelde van
gram zwaar is; iets minder dan het gewone gemiddelde van 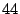 en
en 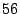 .
Toch mogen we
.
Toch mogen we
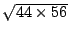 met even veel recht een gemiddelde van
met even veel recht een gemiddelde van 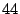 en
en 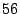 noemen; het wordt het meetkundig gemiddelde van de
twee getallen genoemd.
Ter onderscheidt noemen we het `gewone' gemiddelde daarom het
rekenkundig gemiddelde.
Het rekenkundig gemiddelde treedt op in situaties waarin je optelt;
als je twee touwtjes hebt van lengte
noemen; het wordt het meetkundig gemiddelde van de
twee getallen genoemd.
Ter onderscheidt noemen we het `gewone' gemiddelde daarom het
rekenkundig gemiddelde.
Het rekenkundig gemiddelde treedt op in situaties waarin je optelt;
als je twee touwtjes hebt van lengte 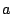 en
en 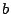 dan zijn twee touwtjes van
lengte
dan zijn twee touwtjes van
lengte 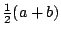 samen even lang als de oorspronkelijke touwtjes samen.
Het meetkundig gemiddelde heeft met vermenigvuldigen te maken: een
rechthoek met zijden
samen even lang als de oorspronkelijke touwtjes samen.
Het meetkundig gemiddelde heeft met vermenigvuldigen te maken: een
rechthoek met zijden 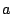 en
en 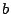 heeft een even grote oppervlakte als een
vierkant met (even lange) zijden
heeft een even grote oppervlakte als een
vierkant met (even lange) zijden 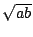 .
.
Opgave.
Als je twee weerstanden 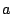 en
en 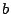 in serie schakelt is de totale weerstand
hun som, de gemiddelde weerstand is dus het rekenkundig gemiddelde.
Als je ze parallel schakelt dan geldt voor de totale weestand
in serie schakelt is de totale weerstand
hun som, de gemiddelde weerstand is dus het rekenkundig gemiddelde.
Als je ze parallel schakelt dan geldt voor de totale weestand 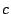 de volgende formule:
de volgende formule:
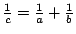 .
Hoe ziet in deze situatie de gemiddelde weerstand er uit?
(Dit gemiddelde heet het harmonisch gemiddelde van
.
Hoe ziet in deze situatie de gemiddelde weerstand er uit?
(Dit gemiddelde heet het harmonisch gemiddelde van 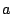 en
en 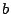 .)
.)



Next: Een ongelijkheid
Up: augustus-1
Previous: augustus-1
Klaas Pieter Hart
2001-05-31
![]() en
en ![]() in serie schakelt is de totale weerstand
hun som, de gemiddelde weerstand is dus het rekenkundig gemiddelde.
Als je ze parallel schakelt dan geldt voor de totale weestand
in serie schakelt is de totale weerstand
hun som, de gemiddelde weerstand is dus het rekenkundig gemiddelde.
Als je ze parallel schakelt dan geldt voor de totale weestand ![]() de volgende formule:
de volgende formule:
![]() .
Hoe ziet in deze situatie de gemiddelde weerstand er uit?
(Dit gemiddelde heet het harmonisch gemiddelde van
.
Hoe ziet in deze situatie de gemiddelde weerstand er uit?
(Dit gemiddelde heet het harmonisch gemiddelde van ![]() en
en ![]() .)
.)