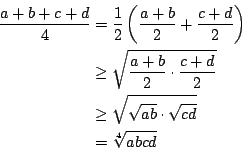Next: Toepassingen
Up: augustus-1
Previous: Een ander gemiddelde
De Franse wiskundige Cauchy vond de relatie tussen 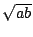 en
en
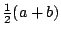 belangrijk genoeg om hem apart als stelling te vermelden:
belangrijk genoeg om hem apart als stelling te vermelden:
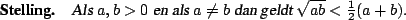
Het was dus geen toeval dat onze brief iets minder dan 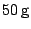 woog.
Het bewijs van de ongelijkheid is niet moeilijk als je eerst naar de brief kijkt:
woog.
Het bewijs van de ongelijkheid is niet moeilijk als je eerst naar de brief kijkt:
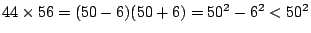 en dus
en dus
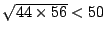 .
Als je nu willekeurige
.
Als je nu willekeurige 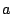 en
en 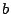 invult krijg je
invult krijg je
en dus
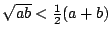 .
De stelling staat bekend als de ongelijkheid van Rekenkundig en Meetkundig
Gemiddelde.
Omdat, natuurlijk,
.
De stelling staat bekend als de ongelijkheid van Rekenkundig en Meetkundig
Gemiddelde.
Omdat, natuurlijk,
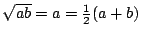 als
als 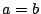 formuleren
we de ongelijkheid ook wel als:
voor elke tweetal positieve getallen
formuleren
we de ongelijkheid ook wel als:
voor elke tweetal positieve getallen 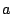 en
en 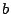 geldt
geldt
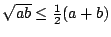 , waarbij gelijkheid geldt precies dan als
, waarbij gelijkheid geldt precies dan als 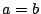 .
.
Opgave.
Wat is de relatie tussen het harmonische gemiddelde en de andere gemiddelden?
Cauchy stopte niet bij twee getallen; hij zag in dat de ongelijkheid
ook voor grotere aantallen geldt.
Bijvoorbeeld voor vier getallen 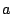 ,
, 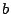 ,
, 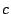 en
en 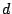 :
:
Voor drie getallen 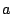 ,
, 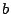 en
en 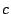 paste hij een kunstgreep toe:
stel
paste hij een kunstgreep toe:
stel
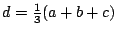 en pas het geval voor vier getallen toe:
en pas het geval voor vier getallen toe:
Maar 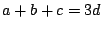 , dus er staat eigenlijk
, dus er staat eigenlijk 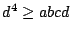 ; deel
; deel 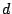 weg
en we vinden
weg
en we vinden 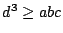 en dus
en dus
In beide gevallen treedt gelijkheid op precies dan als de getallen allemaal aan
elkaar gelijk zijn.
Opgave.
Hoe zou je de ongelijkheid voor rekenkundig en meetkundig gemiddelde
bewijzen voor zeven getallen?
En voor een willekeurig aantal getallen?



Next: Toepassingen
Up: augustus-1
Previous: Een ander gemiddelde
Klaas Pieter Hart
2001-05-31
![]() ,
, ![]() ,
, ![]() en
en ![]() :
: