


Next: Nog twee reeksen
Up: juni-1
Previous: juni-1
In het februarinummer van Pythagoras hebben we gezien dat
Als nu
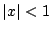 dan kunnen we
dan kunnen we
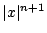 net zo klein maken als we
willen door
net zo klein maken als we
willen door 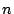 maar groot genoeg te nemen.
We zeggen wel ``
maar groot genoeg te nemen.
We zeggen wel ``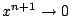 als
als 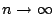 ''; maar dan ook
''; maar dan ook
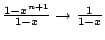 als
als 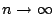 .
Dit schrijven we dan weer als
.
Dit schrijven we dan weer als
Hier staat een formule voor een som van oneindig veel getallen.
Klaas Pieter Hart
2001-04-25