


Next: About this document ...
Up: juni-1
Previous: De reeks met kwadraten
Isaac Newton had ontdekt dat je 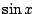 als een oneindige som van machten
van
als een oneindige som van machten
van 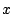 kunt schrijven::
kunt schrijven::
Euler deelde links en rechts door 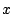 :
:
Dit is een functie die in 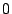 de waarde
de waarde 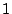 aanneemt en die verder
aanneemt en die verder
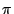 ,
, 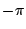 ,
, 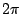 ,
, 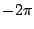 , ...,
, ..., 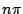 ,
, 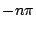 , ... als nulpunten
heeft.
Wat Euler wist was dat als je van een functie
, ... als nulpunten
heeft.
Wat Euler wist was dat als je van een functie 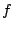 vastlegt wat de
nulpunten zijn, dat
vastlegt wat de
nulpunten zijn, dat 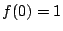 , en dat
, en dat 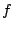 als som van machten van
als som van machten van 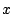 te
schrijven is dan ligt
te
schrijven is dan ligt 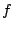 helemaal vast.
helemaal vast.
Bijvoorneeld als we willen dat 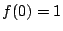 , dat
, dat 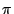 ,
, 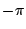 ,
, 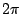 en
en 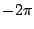 precies de nulpunten van
precies de nulpunten van 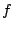 zijn en dat
zijn en dat 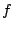 als som van machten
van
als som van machten
van 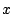 te schrijven is dan moeten we wel
te schrijven is dan moeten we wel
nemen.
Dit kunnen we omwerken tot
als we dit verder uitvermenigvuldigen komt er
Merk op dat tussen de haakjes voor de 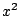 precies
precies
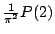 staat.
staat.
Als je precies 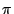 ,
, 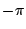 ,
, 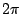 ,
, 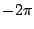 , ...,
, ..., 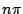 ,
, 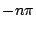 als nulpunten wilt en
als nulpunten wilt en 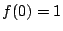 dan kom je, op dezelfde manier, uit op
dan kom je, op dezelfde manier, uit op
en als je dat weer uitwerkt komt er
ofwel
Als we nu 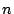 laten groeien dan moeten we, wegens het uniek zijn van de
functie, uiteindelijk op
laten groeien dan moeten we, wegens het uniek zijn van de
functie, uiteindelijk op
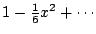 uitkomen.
Conclusie:
uitkomen.
Conclusie:
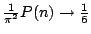 , ofwel
, ofwel
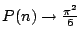 ,
als
,
als 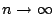 en dat is nou precies wat we wilden weten.
en dat is nou precies wat we wilden weten.



Next: About this document ...
Up: juni-1
Previous: De reeks met kwadraten
Klaas Pieter Hart
2001-04-25
![]() als een oneindige som van machten
van
als een oneindige som van machten
van ![]() kunt schrijven::
kunt schrijven::
![]() , dat
, dat ![]() ,
, ![]() ,
, ![]() en
en ![]() precies de nulpunten van
precies de nulpunten van ![]() zijn en dat
zijn en dat ![]() als som van machten
van
als som van machten
van ![]() te schrijven is dan moeten we wel
te schrijven is dan moeten we wel
![]() ,
, ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() als nulpunten wilt en
als nulpunten wilt en ![]() dan kom je, op dezelfde manier, uit op
dan kom je, op dezelfde manier, uit op