


Next: Euler's afleiding
Up: juni-1
Previous: De harmonische reeks
Hoe zit het met de 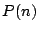 ?
Deze getallen groeien ook maar er is een grens aan hun groei.
De gebroeders Bernoulli konden met behulp van het volgende trucje
zo'n grens aangeven:
?
Deze getallen groeien ook maar er is een grens aan hun groei.
De gebroeders Bernoulli konden met behulp van het volgende trucje
zo'n grens aangeven:
en dus is
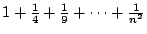 kleiner dan
kleiner dan
Conclusie:
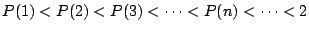 .
.
Er moet dus een getal 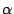 zijn met de eigenschap dat
zijn met de eigenschap dat 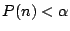 voor
alle
voor
alle 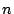 , én zo dat voor elk kleiner getal
, én zo dat voor elk kleiner getal 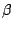 er een
er een 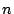 is met
is met
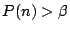 .
Dat getal
.
Dat getal 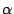 is dan de waarde van de oneindige som
is dan de waarde van de oneindige som
Maar wat is die 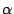 dan?
Rond 1734 ontdekte Leonhard Euler dat
dan?
Rond 1734 ontdekte Leonhard Euler dat
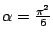 en gaf ons
daarmee de volgende fraaie formule
en gaf ons
daarmee de volgende fraaie formule
In de volgende paragraaf zal ik uitleggen hoe Euler deze formule vond.
Dat zal niet makkelijk zijn maar wie mee durft te gaan voorbij de drie rondjes
krijgt een van de mooiste redeneringen uit de wiskunde te zien.
Klaas Pieter Hart
2001-04-25
![]() ?
Deze getallen groeien ook maar er is een grens aan hun groei.
De gebroeders Bernoulli konden met behulp van het volgende trucje
zo'n grens aangeven:
?
Deze getallen groeien ook maar er is een grens aan hun groei.
De gebroeders Bernoulli konden met behulp van het volgende trucje
zo'n grens aangeven:
![]() zijn met de eigenschap dat
zijn met de eigenschap dat ![]() voor
alle
voor
alle ![]() , én zo dat voor elk kleiner getal
, én zo dat voor elk kleiner getal ![]() er een
er een ![]() is met
is met
![]() .
Dat getal
.
Dat getal ![]() is dan de waarde van de oneindige som
is dan de waarde van de oneindige som