


Next: De e-macht
Up: Analyse volgens Newton
Previous: Analyse volgens Newton
Verderop in het artikel pakte Newton een ander probleem aan:
'vind de basis, 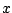 , als de oppervlakte,
, als de oppervlakte, 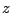 , gegeven is'.
Dit is een natuurlijke vraag en het was vooral hier dat de
vergelijkingen met oneindig veel termen hun nut bewezen.
, gegeven is'.
Dit is een natuurlijke vraag en het was vooral hier dat de
vergelijkingen met oneindig veel termen hun nut bewezen.
Zijn eerste voorbeeld was meteen de hyperbool en hij liet zien hoe je
de vergelijking
naar 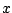 kunt oplossen.
Dat deed hij door de vergelijking met de volgende deelvergelijkingen
te benaderen:
kunt oplossen.
Dat deed hij door de vergelijking met de volgende deelvergelijkingen
te benaderen:
Vervolgens loste hij die deelvergelijkingen op.
De eerste is geen kunst:  .
De oplossing van de tweede vergelijking zou een verbetering van de oplossing
van de eerste moeten zijn.
Daarom schreef Newton
.
De oplossing van de tweede vergelijking zou een verbetering van de oplossing
van de eerste moeten zijn.
Daarom schreef Newton 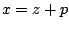 en vulde hij dat in:
en vulde hij dat in:
Wegstrepen van 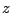 en toepassing van de
en toepassing van de  -formule geeft ons
-formule geeft ons
Nu moet 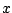 bijna
bijna 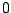 zijn als
zijn als 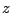 dat is, dus moeten we
dat is, dus moeten we
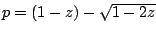 hebben.
Newton had intussen al laten zien hoe je
hebben.
Newton had intussen al laten zien hoe je 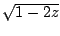 tot een
oneindige som kunt ombouwen:
tot een
oneindige som kunt ombouwen:
Daarmee vond hij
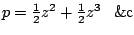 .
.
Opgave 2.
Kwadrateer
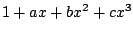 , stel het resultaat gelijk aan
, stel het resultaat gelijk aan 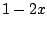 en bepaal zo
en bepaal zo 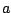 ,
, 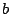 en
en 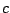 .
.
Omdat hij met een kwadratische vergelijking begon, wist Newton dat hij
de 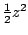 wel kon vertrouwen, maar de
wel kon vertrouwen, maar de 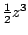 nog niet.
nog niet.
Daarom schreef hij
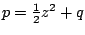 (en dus
(en dus
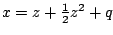 )
en vulde dat in in de derde vergelijking.
Het werkt makkelijker als je eerst
)
en vulde dat in in de derde vergelijking.
Het werkt makkelijker als je eerst 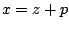 invult en de voorgaande stappen
over doet maar nu met
invult en de voorgaande stappen
over doet maar nu met
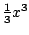 erbij.
Na invullen en wegstrepen hou je dan het volgende over:
erbij.
Na invullen en wegstrepen hou je dan het volgende over:
Als we nu
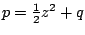 invullen, valt de
invullen, valt de
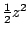 weg en blijft
het volgende over:
weg en blijft
het volgende over:
we hebben alleen 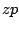 uitgewerkt omdat de andere producten hogere machten
van
uitgewerkt omdat de andere producten hogere machten
van 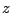 dan de derde opleveren.
Dit wist Newton ook en hij interpreteerde het resultaat
daarom als volgt:
dan de derde opleveren.
Dit wist Newton ook en hij interpreteerde het resultaat
daarom als volgt:
(De 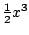 was inderdaad niet betrouwbaar.)
was inderdaad niet betrouwbaar.)
De volgende stap laat zich nu raden: stel
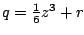 en gebruik de
vierde vergelijking.
Het kost wat moeite, maar je vindt dan
en gebruik de
vierde vergelijking.
Het kost wat moeite, maar je vindt dan
Daarmee heb je dan al de volgende benadering van 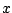 te pakken:
te pakken:
In zijn artikel ging Newton nog één stap verder:
Hij moet op kladpapier nog een stuk doorgerekend hebben, want even later
beschrijft hij hoe het verder zal gaan met deze benaderingen:
de 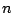 -de macht van
-de macht van 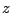 moet gedeeld worden door het product van de getallen
moet gedeeld worden door het product van de getallen
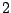 ,
, 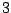 , tot en met
, tot en met 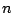 .
.
Conclusie, als je wilt weten bij welke 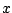 de oppervlakte onder
de grafiek van
de oppervlakte onder
de grafiek van 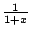 gelijk is aan
gelijk is aan 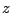 , dan is dat
, dan is dat



Next: De e-macht
Up: Analyse volgens Newton
Previous: Analyse volgens Newton
KP Hart
2005-06-01
![]() , als de oppervlakte,
, als de oppervlakte, ![]() , gegeven is'.
Dit is een natuurlijke vraag en het was vooral hier dat de
vergelijkingen met oneindig veel termen hun nut bewezen.
, gegeven is'.
Dit is een natuurlijke vraag en het was vooral hier dat de
vergelijkingen met oneindig veel termen hun nut bewezen.
![]() , stel het resultaat gelijk aan
, stel het resultaat gelijk aan ![]() en bepaal zo
en bepaal zo ![]() ,
, ![]() en
en ![]() .
.
![]() wel kon vertrouwen, maar de
wel kon vertrouwen, maar de ![]() nog niet.
nog niet.
![]() (en dus
(en dus
![]() )
en vulde dat in in de derde vergelijking.
Het werkt makkelijker als je eerst
)
en vulde dat in in de derde vergelijking.
Het werkt makkelijker als je eerst ![]() invult en de voorgaande stappen
over doet maar nu met
invult en de voorgaande stappen
over doet maar nu met
![]() erbij.
Na invullen en wegstrepen hou je dan het volgende over:
erbij.
Na invullen en wegstrepen hou je dan het volgende over:
![]() en gebruik de
vierde vergelijking.
Het kost wat moeite, maar je vindt dan
en gebruik de
vierde vergelijking.
Het kost wat moeite, maar je vindt dan
![]() de oppervlakte onder
de grafiek van
de oppervlakte onder
de grafiek van ![]() gelijk is aan
gelijk is aan ![]() , dan is dat
, dan is dat