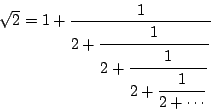In het laatste hoofdstuk van het boek hield Euler zich bezig met zogeheten kettingbreuken. Die ontstaan als je het algoritme van Euclides (zie aan het eind) toepast op paren getallen om hun grootste gemene deler te vinden.
Zijn eerste voorbeeld was de breuk
![]() .
Wat het algoritme van Euclides doet is herhaald delen, waarbij je
telkens quotiënt en rest onthoud.
In de eerste stap vinden we
.
Wat het algoritme van Euclides doet is herhaald delen, waarbij je
telkens quotiënt en rest onthoud.
In de eerste stap vinden we
![]() , of
, of
![]() .
Vervolgens kijken we naar de breuk
.
Vervolgens kijken we naar de breuk ![]() , daar vinden we
, daar vinden we
![]() en dus
en dus
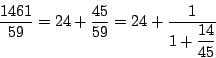
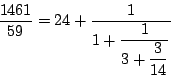
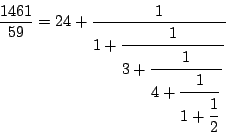
Voor gewone breuken zijn dergelijke schrijfwijzen niet zo opwindend,
behalve dan dat de getallen ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() en
en ![]() heel wat kleiner
zijn dan
heel wat kleiner
zijn dan ![]() en
en ![]() .
.
Voor getallen die niet als een breuk te schrijven zijn, zoals ![]() ,
,
![]() en
en ![]() kun je kettingbreuken gebruiken om heel nauwkeurige benaderingen
te maken.
Voor
kun je kettingbreuken gebruiken om heel nauwkeurige benaderingen
te maken.
Voor ![]() gaf Euler de volgende uitdrukking:
gaf Euler de volgende uitdrukking: