Een formule voor e

Van Euler wordt gezegd dat hij rekende zoals anderen ademhaalden. Door al dat werk kwam hij verbanden op het spoor die anderen niet zagen. Zo vond hij voor $\mathrm{e}$ ook een kettingbreuk, niet rechtstreeks maar via de breuk $\frac{\mathrm{e}-1}2$. Hij begon met de benadering $\mathrm{e}\approx2{,}718281828459$ en werkte die om tot $\frac{\mathrm{e}-1}2\approx0{,}8591409142295$ Daarna voerde hij de delingen als boven uit voor het quotiënt $\frac{10000000000000}{8591409142295}$:

$$\vcenter{\openup2\jot \let\dsp\displaystyle \halign{\hfil$\... ...c{551438155}{25010204} &=&22&+&\frac{12113667}{25010204}\cr }}$$

Dat rekenwerk leverde de volgende kettingbreuk

$$\frac{\mathrm{e}-1}2= {1\over\displaystyle 1+{\strut1\over\... ...r\displaystyle 18+{\strut1\over\displaystyle 22+\cdots}}}}}}$$

Euler schreef hier doodleuk bij: met betere benaderingen van $\mathrm{e}$ hadden we het rijtje $1$, $6$, $10$, $14$, $18$, $22$, $26$, $30$, $34$, ... (met $4k-2$ op de $k$-de plaats) gevonden. De partiële breuken die je zo krijgt leveren heel nauwkeurige benaderingen van $\frac12(\mathrm{e}-1)$ en daarmee ook van $\mathrm{e}$ zelf.

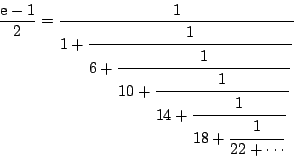
Het uitwerken van zo'n (partiële) kettingbreuk lijkt een heel karwei. In de bovengevonden breuk moeten we beneden beginnen met $18+\frac1{22}=\frac{397}{22}$, dan $14+\frac{22}{397}=\frac{5580}{397}$, dan $10+\frac{397}{5580}$, enzovoort. Dat is een heel gedoe en je moet voor iedere volgende breuk weer helemaal opnieuw beginnen.

Gelukkig bestaat er een relatie tussen de tellers en de noemers van de opeenvolgende breuken. De eerste breuk is $\frac11$ (niet vereenvoudigen), de volgende is $\frac67$, de derde is $\frac{61}{71}$. Let nu op: er geldt $61=1+10\cdot6$ en $71=1+10\cdot7$; de volgende breuk is $\frac{860}{1001}$, waarbij geldt $860=6+14\cdot61$ en $1001=7+14\cdot71$. De volgende in de rij is

$$\frac{61+18\cdot860}{71+18\cdot1001}=\frac{15541}{18089}.$$

In het algemeen: de breuk die je krijgt als je bij $4k-2$ stopt ontstaat als volgt uit de voorgaande twee breuken $\frac pq$ en $\frac rs$:

$$\frac{p+r(4k-2)}{q+s(4k-2)}.\eqno(*)$$

Als je vóór de breuk $\frac11$ nog $\frac 01$ in de rij zet geldt de formule ook voor $k=2$.

Opgave: Om breuken voor $\mathrm{e}$ te krijgen moet je de breuken voor $\frac{\mathrm{e}-1}2$ met $2$ vermenigvuldigen en dan bij het resultaat $1$ optellen. Ga na dat je hetzelfde resultaat krijgt als je met de breuken $\frac 01$ en $\frac31$ begint en vervolgens weer formule $(*)$ gebruikt.