Het algoritme van Euclides

In De Elementen van Euclides staat, in Boek IX, de volgende stelling (de vertaling komt uit een Nederlandse uitgave uit 1930 van E. J. Dijksterhuis):

Wanneer, als twee ongelijke getallen uitgezet zijn, en het kleinste wordt voortdurend van het grootste afgetrokken, het overblijvende nooit het daaraan voorafgaande meet, totdat de eenheid is overgebleven, dan zullen de oorspronkelijke getallen onderling priem zijn.

Dat klinkt wat merkwaardig, maar je moet het meetkundig lezen. Euclides werkte altijd met lijnstukjes, net zoveel eenheden lang als de getallen groot waren. In dit verband betekent `meten' dat het kleinere lijnstuk een geheel aantal malen in het grotere past en dus dat het kleinere getal het grotere deelt.

Als voorbeeld nemen we $8$ en $3$. Trek $3$ van $8$ af, dan blijft $5$ over, dat is groter dan $3$, trek $3$ nogmaals af, dan blijft $2$ over. Nu is $3$ de grootste, trek daar $2$ van af, dan blijft $1$ over. Nu is op geen enkel moment wat overblijft een deler van het voorgaande getal totdat we $1$ (de eenheid) bereikt hebben. Conclusie: $8$ en $3$ zijn relatief priem. Zie figuur 1.

Meteen daarna gebruikte Euclides het bewijs van die stelling om de grootste gemene deler van twee getallen te vinden. Hij merkte namelijk op dat als het wel gebeurt dat ``wat overblijft het voorafgaande meet'' op dat moment de grootste gemene deler van de twee getallen gevonden is.

De grootste gemene deler, $\mathop{\mathrm{ggd}}\nolimits$, van twee getallen is wat de naam zegt: het is een deler van beide getallen en het is het grootste getal met die eigenschap. Het algoritme van Euclides geeft een efficiënte manier om die grootste gemene deler te vinden, bijvoorbeeld $\mathop{\mathrm{ggd}}\nolimits (54,20)$.

Je trekt $20$ twee keer van $54$ af, met rest $14$; die laatste deelt $20$ niet. We gaan door: trek $14$ van $20$ af, met rest $6$; omdat $6$ geen deler van $14$ is doen we nog een stap: trek $6$ twee keer van $14$ af met rest $2$. Omdat $2$ een deler van $6$ is hebben we de grootste gemene deler van $54$ en $20$ gevonden: $\mathop{\mathrm{ggd}}\nolimits (54,20)=2$.

Het algoritme laat zich goed begrijpen door er meetkundig naar te kijken. Neem een rechthoek van $20$ bij $54$ en probeer deze te betegelen met allemaal even grote vierkanten. De zijde van het grootste vierkant dat je hierbij kunt gebruiken is nu net de grootste gemene deler van $20$ en $54$. Die grootste tegelmaat kun je vinden door stapsgewijs vierkanten van de rechthoek af te halen tot er uiteindelijk alleen nog een vierkant overblijft. Eigenlijk precies wat we volgens het algoritme moesten doen. Hiernaast zie je het proces uitgevoerd voor de rechthoek van $20$ bij $54$.

Tegenwoordig wordt het algoritme als volgt beschreven met delen in plaats van aftrekken: ``blijf de grootste door de kleinste delen tot de deling opgaat'', dan heb je de grootste gemene deler te pakken.

We bekijken de getallen die Euler gebruikte nog een keer: de onderstaande reeks delingen laat zien dat $\mathop{\mathrm{ggd}}\nolimits (1461,59)=1$.

$$\vcenter{\normalbaselines\openup1\jot \halign{\hfil$ ...$$

Bij de deling die uiteindelijk opgaat is $1$ de deler en dat is gelijk de grootste gemene deler: $\mathop{\mathrm{ggd}}\nolimits (1461,59)=1$.

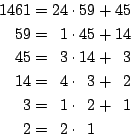
Opgave Bepaal op dezelfde manier de grootste gemene deler van $1461$ en $57$.

Figure: $\mathop{\mathrm{ggd}}\nolimits (8,3)=1$