


Next: Het algoritme van Euclides
Up: Euler over het getal
Previous: Euler's weg naar de
De 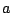 die bij
die bij 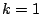 hoort neemt natuurlijk een speciale plaats in.
Die is gelijk aan
hoort neemt natuurlijk een speciale plaats in.
Die is gelijk aan
Als we de breuken uitwerken en optellen, zei Euler, dan krijgen we
waarbij het laatste cijfer echt klopt.
Op dit punt voerde Euler de letter in die wij nu nog voor dit getal
gebruiken: ``het getal dat bij 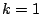 hoort duiden we in het vervolg
kortweg met de letter
hoort duiden we in het vervolg
kortweg met de letter 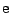 aan''.
Dus
aan''.
Dus
Hiermee hebben we ook, langs een nieuwe weg, de formule voor 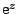 ontdekt
die we in het vorige nummer op de manier van Newton hadden gevonden:
ontdekt
die we in het vorige nummer op de manier van Newton hadden gevonden:
KP Hart
2005-06-03
![]() die bij
die bij ![]() hoort neemt natuurlijk een speciale plaats in.
Die is gelijk aan
hoort neemt natuurlijk een speciale plaats in.
Die is gelijk aan
![]() hoort duiden we in het vervolg
kortweg met de letter
hoort duiden we in het vervolg
kortweg met de letter ![]() aan''.
Dus
aan''.
Dus