Integreren en differenti"eren

Met een beetje kennis van de differentiaal- en integraalrekening kun je goede benaderingen van $\sin x$ en $\cos x$ maken; het voordeel van die benaderingen is dat je ze behulp van alleen optellen, aftrekken, vermenigvuldigen en delen kunt uitrekenen. We leiden de formules alleen voor positieve $x$ af; voor negatieve $x$ gebruiken we natuurlijk dat $\sin (-x)=-\sin x$ en $\cos (-x)=\cos x$.

Wat we van onze functies gebruiken is niet veel: we moeten weten wat hun afgeleiden zijn: $(\sin x)'=\cos x$ en $(\cos x)'=-\sin x$. Deze formules zetten we om in formules voor integralen:

$$\int_0^x\cos t\,\mathrm{d}t=\sin x$$

en

$$\int_0^x\sin t\,\mathrm{d}t=1-\cos x;$$

de laatste kunnen we ook schrijven als

$$\cos x=1-\int_0^x\sin t\,\mathrm{d}t.$$

Verder gebruiken we nog dat $\cos x<1$ (behalve als $x=2k\pi$ met $k\in\mathbb{N}$ natuurlijk).

Met behulp van $\cos x<1$ vinden we namelijk

$$\sin x=\int_0^x\cos t\,\mathrm{d}t<\int_0^x1\,\mathrm{d}t=x,$$

dit geldt voor alle $x>0$.

Maar dan volgt op dezelfde manier

$$\cos x=1-\int_0^x\sin t\,\mathrm{d}t > 1-\int_0^x t\,\mathrm{d}t =1-\frac12x^2,$$

weer voor alle $x>0$.

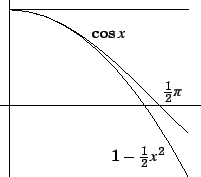
Als we weer terug gaan naar $\sin x$ vinden we

$$\sin x > \int_0^x 1-\frac12t^2\,\mathrm{d}t=x-\frac16x^3.$$

Dit stoppen we weer in de integraal voor $\cos x$:

$$\cos x< 1 -\int_0^x t-\frac16t^3\,\mathrm{d}t = 1-\frac12x^2+\frac1{24}x^4$$

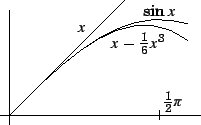
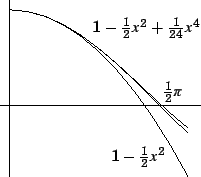
Voor we nog verder gaan bekijken we even wat we gevonden hebben. Blijkbaar geldt, voor $x>0$, dat

$$x-\frac16x^3<\sin x <x$$

en

$$1-\frac12x^2<\cos x<1-\frac12x^2+\frac1{24}x^4\eqno(*)$$

Dit geeft voor niet al te grote $x$ al redelijk scherpe benaderingen, bijvoorbeeld $\sin0{,}2\approx0{,}2$ met een afwijking van minder dan $0{,}008/6=0{,}00133\ldots$. Voor $\cos0{,}2$ krijgen we de benadering $0{,}98$ met een afwijking van minder dan $0{,}00066\ldots$.

Opgave. Op welk interval vindt je het nog acceptabel om $\sin x$ met $x$ te benaderen? En voor welke $x$ ben je tevreden met $1-\frac12x^2$ als benadering van $\cos x$?