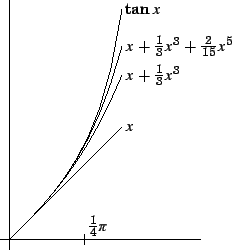Next: About this document ...
Up: en
Previous: Wanneer stoppen we?
Nu we toch bezig zijn kunnen we gelijk een knop voor 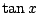 proberen
te maken.
We kunnen natuurlijk onder die knop gewoon het quotiënt van
proberen
te maken.
We kunnen natuurlijk onder die knop gewoon het quotiënt van 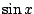 en
en 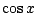 programmeren maar we kunnen ook proberen een eenvoudige som
van machten van
programmeren maar we kunnen ook proberen een eenvoudige som
van machten van 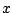 te maken.
De reden hiervoor is dat we zo het aantal rekenstappen kunnen beperken;
in plaats van twee keer een som van zes machten van
te maken.
De reden hiervoor is dat we zo het aantal rekenstappen kunnen beperken;
in plaats van twee keer een som van zes machten van 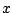 uit te rekenen
(en op elkaar te delen) kunnen we misschien met één zo'n berekening
toe.
Hiertoe delen we de benaderingen van
uit te rekenen
(en op elkaar te delen) kunnen we misschien met één zo'n berekening
toe.
Hiertoe delen we de benaderingen van 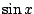 en
en 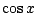 (voor ons rekenmachientje in aanbouw) op elkaar.
(voor ons rekenmachientje in aanbouw) op elkaar.
Met enig doorzettingsvermogen levert een staartdeling
de volgende benadering voor 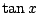 :
:
Het verschil tussen 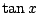 en deze benadering laat zich niet zo makkelijk
afschatten als bij
en deze benadering laat zich niet zo makkelijk
afschatten als bij 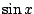 en
en 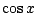 .
Dat ligt aan een paar dingen, waaronder
.
Dat ligt aan een paar dingen, waaronder 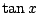 zelf: op het interval
zelf: op het interval
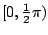 is de benadering netjes begrensd maar de tangens heeft
bij
is de benadering netjes begrensd maar de tangens heeft
bij 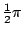 een verticale asymptoot.
Maar ook op het interval
een verticale asymptoot.
Maar ook op het interval
![$[0,\frac14\pi]$](img45.png) is de laatste benadering niet
zo goed als die van de sinus en cosinus; dat komt doordat we
benaderingen op elkaar gedeeld hebben en ook nog eens een rest bij die
deling weggelaten hebben.
Al met al krijgen we met bovenstaande formule maar drie betrouwbare
cijfers achter de komma.
is de laatste benadering niet
zo goed als die van de sinus en cosinus; dat komt doordat we
benaderingen op elkaar gedeeld hebben en ook nog eens een rest bij die
deling weggelaten hebben.
Al met al krijgen we met bovenstaande formule maar drie betrouwbare
cijfers achter de komma.
Met een slimmigheidje kun je dat dramatisch verbeteren;
gebruik hiervoor de verdubbelingsformule voor de tangens:
Dit gebruik je als volgt: begin met
![$x\in[0,\frac14\pi]$](img65.png) ,
benader
,
benader 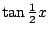 , noem de benadering
, noem de benadering 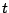 , en gebruik dan
, en gebruik dan 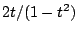 als benadering van
als benadering van 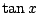 zelf.
Dat levert gelijk zeven betrouwbare cijfers achter de komma op.
zelf.
Dat levert gelijk zeven betrouwbare cijfers achter de komma op.




Next: About this document ...
Up: en
Previous: Wanneer stoppen we?
KP Hart
2005-08-26
![]() proberen
te maken.
We kunnen natuurlijk onder die knop gewoon het quotiënt van
proberen
te maken.
We kunnen natuurlijk onder die knop gewoon het quotiënt van ![]() en
en ![]() programmeren maar we kunnen ook proberen een eenvoudige som
van machten van
programmeren maar we kunnen ook proberen een eenvoudige som
van machten van ![]() te maken.
De reden hiervoor is dat we zo het aantal rekenstappen kunnen beperken;
in plaats van twee keer een som van zes machten van
te maken.
De reden hiervoor is dat we zo het aantal rekenstappen kunnen beperken;
in plaats van twee keer een som van zes machten van ![]() uit te rekenen
(en op elkaar te delen) kunnen we misschien met één zo'n berekening
toe.
Hiertoe delen we de benaderingen van
uit te rekenen
(en op elkaar te delen) kunnen we misschien met één zo'n berekening
toe.
Hiertoe delen we de benaderingen van ![]() en
en ![]() (voor ons rekenmachientje in aanbouw) op elkaar.
(voor ons rekenmachientje in aanbouw) op elkaar.
![]() :
: