
Definition.
Orthogonality. If 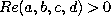 and non-real parameters
occur in conjugate pairs, then
and non-real parameters
occur in conjugate pairs, then
where
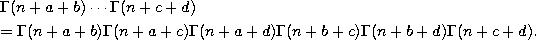
If a < 0 and a+b, a+c, a+d are positive or a pair of complex conjugates occur with positive real parts, then
Recurrence relation.
where
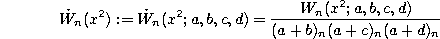
and
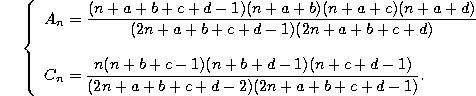
Normalized recurrence relation.
where

Difference equation.
where
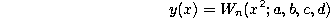
and
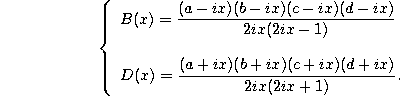
Forward shift operator.
or equivalently
Backward shift operator.
or equivalently
where
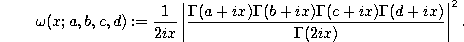
Rodrigues-type formula.
Generating functions.
Remark. If we set
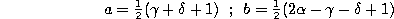
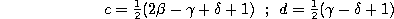
and

in
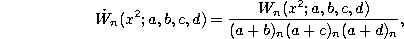
defined by (1.1.1) and take

we obtain the Racah polynomials defined by (1.2.1).
References. [43], [63], [64], [67], [225], [226], [273], [274], [312], [317], [391], [399], [400].