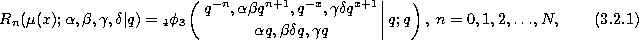
Definition.
where
and
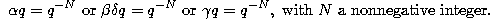
Since
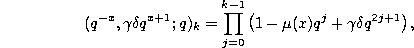
it is clear that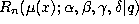 
is a polynomial
of degree n in 
.
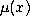Orthogonality.
where
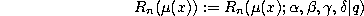
and
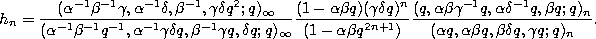
This implies
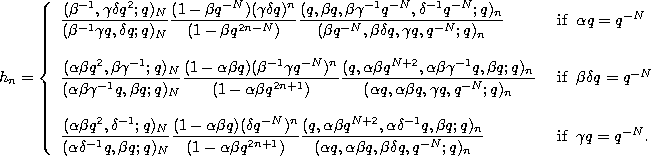
Recurrence relation.
where
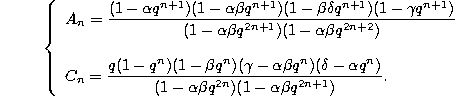
Normalized recurrence relation.
where
q-Difference equation.
where
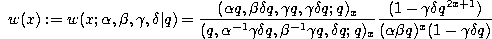
and 
as below. This q-difference equation can also be written in the
form
where
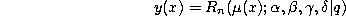
and
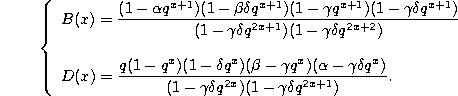
Forward shift operator.
or equivalently
Backward shift operator.
or equivalently
where
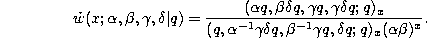
Rodrigues-type formula.
where
Generating functions. For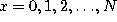 
we have
Remarks.
The Askey-Wilson polynomials defined by (3.1.1) and the q-Racah
polynomials given by (3.2.1) are related in the following way.
If we substitute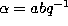 
, 
, 
,
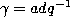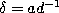and 
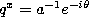in the definition
(3.2.1) of the q-Racah polynomials we find :
and
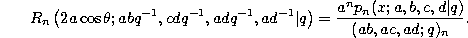
If we change q by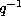 
we find
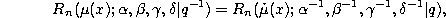
where
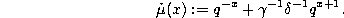
References. [13], [26], [31], [62], [64], [67], [117], [118], [160], [188], [190], [193], [218], [245], [279], [323], [331], [346].
