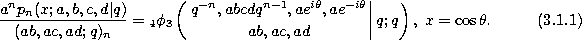
Definition.
The Askey-Wilson polynomials are q-analogues of the Wilson polynomials given by (1.1.1).
Orthogonality. If a,b,c,d are real, or occur in complex conjugate
pairs if complex, and
 , then we have the following orthogonality relation
, then we have the following orthogonality relation
where

with
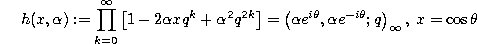
and

If a > 1 and b,c,d are real or one is real and the other two are complex conjugates,
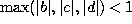 and the pairwise products of a,b,c and d have
absolute value less than one, then we have another orthogonality relation
given by :
and the pairwise products of a,b,c and d have
absolute value less than one, then we have another orthogonality relation
given by :
where  and
and 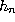 are as before,
are as before,

and
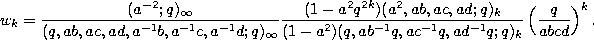
Recurrence relation.
where
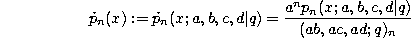
and

Normalized recurrence relation.
where
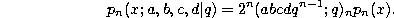
q-Difference equation.
where
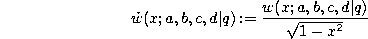
and
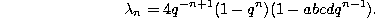
If we define
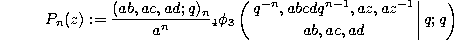
then the q-difference equation can also be written in the form
where
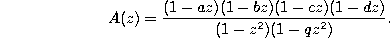
Forward shift operator.
or equivalently
Backward shift operator.
or equivalently
Rodrigues-type formula.
Generating functions.
Remarks.
The q-Racah polynomials defined by (3.2.1) and the Askey-Wilson
polynomials given by (3.1.1) are related in the following way.
If we substitute 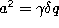 ,
, 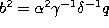 ,
,
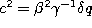 ,
, 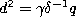 and
and 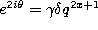 in the definition (3.1.1)
of the Askey-Wilson polynomials we find :
in the definition (3.1.1)
of the Askey-Wilson polynomials we find :

where
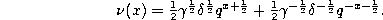
If we change q by 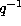 we find
we find
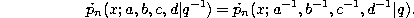
References. [13], [31], [43], [58], [64], [67], [69], [70], [96], [97], [191], [193], [203], [204], [218], [224], [226], [230], [231], [234], [238], [242], [249], [256], [259], [281], [282], [293], [318], [322], [323], [324], [328], [346], [347], [349], [350], [352], [353], [355], [359], [371], [389], [400].