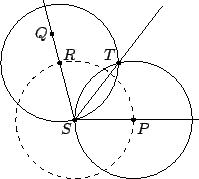
Een ander voorbeeld: de constructie van
een lijn die een gegeven hoek
in twee gelijke hoeken deelt.
De hoek wordt gegeven door twee lijnen
die snijden in een punt ![]() . Verder is op één van de twee lijnen
een tweede punt
. Verder is op één van de twee lijnen
een tweede punt ![]() gegeven.
De constructie gaat als volgt.
Teken een cirkel met als middelpunt
gegeven.
De constructie gaat als volgt.
Teken een cirkel met als middelpunt ![]() en als straal het lijnstuk
en als straal het lijnstuk ![]() .
Deze cirkel snijdt de andere lijn in
.
Deze cirkel snijdt de andere lijn in ![]() .
Teken vervolgens twee cirkels met middelpunten
.
Teken vervolgens twee cirkels met middelpunten ![]() en
en ![]() en straal
en straal ![]() .
Deze cirkels snijden in
.
Deze cirkels snijden in ![]() en een ander punt dat we
en een ander punt dat we ![]() noemen.
Dan deelt het lijnstuk
noemen.
Dan deelt het lijnstuk ![]() de gegeven hoek in twee gelijke hoeken.
de gegeven hoek in twee gelijke hoeken.