


Next: De reeks met kwadraten
Up: juni-1
Previous: Nog twee reeksen
In de veertiende eeuw al ontdekte Nicolas Oresme dat de 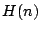 onbeperkt
doorgroeien; hij zag dit in door de som in geschikte groepjes te verdelen
onbeperkt
doorgroeien; hij zag dit in door de som in geschikte groepjes te verdelen
De som van elk apart groepje is meer dan 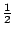 , waarmee we in kunnen zien
dat
, waarmee we in kunnen zien
dat 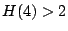 ,
, 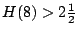 , ...,
, ...,
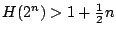 .
Dus de
.
Dus de 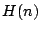 kruipen langzaam maar zeker naar
kruipen langzaam maar zeker naar 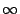 en we vinden
en we vinden
Klaas Pieter Hart
2001-04-25
![]() onbeperkt
doorgroeien; hij zag dit in door de som in geschikte groepjes te verdelen
onbeperkt
doorgroeien; hij zag dit in door de som in geschikte groepjes te verdelen