Een betere schatting

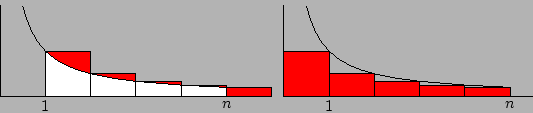
Met wat integraalrekening kunnen we een veel betere schatting van $H(n)$ geven en ook nauwkeuriger bepalen wanneer de slak bij het paard aangekomen zal zijn. Uit het linker plaatje kunnen we gemakkelijk aflezen dat $H(n)$ (rood) groter is dan de oppervlakte onder de grafiek van $y=\frac1x$ tussen $x=1$ en $x=n+1$ en dus zeker groter dan de oppervlakte tussen $x=1$ en $x=n$ -- die oppervlakte noemen we even $O(n)$. Aan de andere kant is $H(n)-1=\frac12+\cdots+\frac1n$ kleiner diezelfde oppervlakte $O(n)$ (zie het rechter plaatje).

$$\centerline{\includegraphics{juni.1}\hss\includegraphics{juni.2}}$$

De waarde van $O(n)$ kunnen we uitrekenen:

$$O(n)=\int_1^n\frac1x\,dx=[\ln x]_1^n=\ln n.$$

We vinden dus $\ln n<H(n)<1+\ln n$. De getallen $H(n)$ stijgen dus net zo snel als de natuurlijke logaritme. Hiermee kunnen we beter afschatten wanneer de slak bij het paard is: nog niet als $\ln n<999$, dat wil zeggen als $n<e^{999}$, maar zeker wel als $\ln n\ge1000$ of wel als $n\ge e^{1000}$.

Opgave. Is $e^{1000}$ een aanzienlijke verbetering ten opzichte van $2^{1998}$?

Leonhard Euler onderzocht het verschil tussen $H(n)$ en $\ln n$; hij ontdekte dat $H(n)-\ln n$ naar een vaste waarde convergeert, die waarde wordt genoteerd met $\gamma$ en is ongeveer $0.5772156649$. Je kunt wereldberoemd worden door vast te stellen of $\gamma$ een breuk is of juist niet.