Aan een spijker

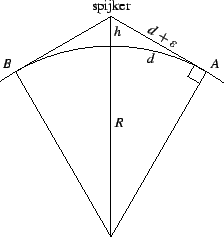
We bekijken nu een ander probleem. Stel dat we het touw alléén aan de Noordpool optillen en strak trekken -- alsof we de aarde met behulp van het touw aan een spijker ophangen -- hoe hoog komt het hoogste punt als we het touw strak omhoog trekken?

Het volgende plaatje geeft een situatieschets.

Hierin is $R$ de straal van de aarde, $\varepsilon$ de helft van het ingelaste stukje (een halve meter dus) en $h$ de gevraagde hoogte. De boog $d$ verbindt de punten waar het touw los komt van het aardoppervlak. De hoek bij $A$ is recht omdat de lijn van $A$ naar de spijker een raaklijn aan de cirkel is, dankzij het straktrekken.

Pas de stelling van Pythagoras toe:

$$(R+h)^2=R^2+(d+\varepsilon )^2$$

en dus $h+R=\pm\sqrt{R^2+(d+\varepsilon )^2}$, ofwel

$$h=-R\pm\sqrt{R^2+(d+\varepsilon )^2}$$

omdat $h$ positief is moeten we

$$h=\sqrt{R^2+(d+\varepsilon )^2}-R$$

hebben. Hierin kunnen we $R$ buiten de haakjes halen, zodat we tot

$$h=R\left(\sqrt{1+\left(\frac{d+\varepsilon }R\right)^2}-1\right) \eqno(*)$$

Hierin is $d$ nog onbekend. Nu geldt $d=\alpha R$ of $\frac dR=\alpha$ (we werken in radialen) en het blijkt wat makkelijker te zijn een vergelijking voor $\alpha$ op te stellen.

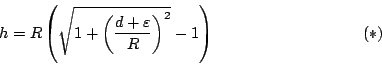
Uit de schets kunnen we aflezen dat

$$\tan\alpha=\frac{d+\varepsilon }R$$

en dus

$$\tan\alpha=\alpha+\frac{\varepsilon }R$$

ofwel

$$\tan\alpha-\alpha=\frac{\varepsilon }R\eqno(\dag )$$

We krijgen $\alpha$ dus als oplossing van de vergelijking $(\dag )$.

Nu wordt het tijd de getallen in te gaan vullen. De omtrek van de Aarde is, per definitie, $40.000\,\mathrm {km}$, zodat $R=40.000.000/(2\pi)\,\mathrm {m}$, verder $\varepsilon =\frac12\,\mathrm {m}$. We moeten dus

$$\tan\alpha-\alpha=\frac\pi{40.000.000}$$

oplossen. Je kunt dit zó door de Solver van de TI-83 laten doen (X=1 als beginvoorwaarde gebruiken): $\alpha\approx0{,}006176=6{,}176\times10^{-3}$ en daarmee $d\approx39{,}32\,\mathrm {km}$. Hoewel het interessant is te zien hoe ver van de noordpool het touw recht wordt hebben we $d$ niet echt nodig voor de berekening; in $(*)$ vervangen we $\frac dR$ door $\alpha$:

$$h=R\left(\sqrt{1+\left(\alpha+\frac{\varepsilon }R\right)^2}-1\right)$$

Mijn rekenmachientje geeft, na alles invullen: $h\approx121{,}4\,\mathrm {m}$.

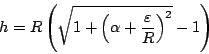
Opgave Doe de berekening nogmaals maar nu met slechts één centimeter extra. Aangenomen dat het touw licht genoeg is, kun je het dan zonder hulpmiddelen strak krijgen?