


Next: About this document ...
Up: Een touwtje om de
Previous: Aan een spijker
De hoek 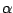 die hierboven gevonden is is behoorlijk klein.
In dat geval kan
die hierboven gevonden is is behoorlijk klein.
In dat geval kan 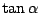 goed benaderd
worden met
goed benaderd
worden met
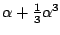 (zie stukje over
(zie stukje over 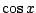 en
en 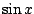 in de vorige Pythagoras),
zodat
in de vorige Pythagoras),
zodat 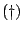 verandert in een bijna-gelijkheid:
verandert in een bijna-gelijkheid:
De breuk
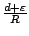 is ook heel klein en voor heel kleine
is ook heel klein en voor heel kleine 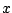 geldt
geldt
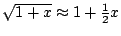 ; daarmee kunnen we
; daarmee kunnen we 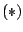 omwerken tot
omwerken tot
Als we het kwadraat uitwerken komt er
Als we de getallen weer invullen krijgen we
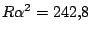 ,
,
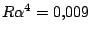 en
en
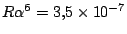 .
Dit betekent dat we de vierde en zesde machten wel weg kunnen laten
en de volgende benadering van
.
Dit betekent dat we de vierde en zesde machten wel weg kunnen laten
en de volgende benadering van 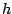 gebruiken:
gebruiken:
Als we verder nog bedenken dat
![$\alpha\approx\sqrt[3]{\frac{3\varepsilon }R}$](img49.png) dan komen we tot de volgende uitdrukking voor
dan komen we tot de volgende uitdrukking voor 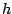 :
:
Als we dan ook nog de waarde van 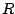 invoeren houden uiteindelijk de
volgende benadering over
invoeren houden uiteindelijk de
volgende benadering over
Dit geeft niet echt een ander antwoord dan de berekening in het begin:
als we
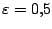 invullen komen we via
invullen komen we via 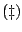 ook uit op
ook uit op
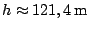 .
.
Opgave
Vul
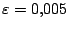 in.
Hoe groot is het verschil ten opzichte van het antwoord op de vorige opgave?
in.
Hoe groot is het verschil ten opzichte van het antwoord op de vorige opgave?
Opgave
Onderzoek hoe goed de benadering
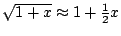 is.
Vergelijk bijvoorbeeld
is.
Vergelijk bijvoorbeeld
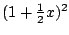 met
met 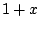 ; voor welke
; voor welke 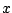 is
het verschil klein genoeg om weg te laten?
Was in ons voorbeeld de benadering gerechtvaardigd?
is
het verschil klein genoeg om weg te laten?
Was in ons voorbeeld de benadering gerechtvaardigd?



Next: About this document ...
Up: Een touwtje om de
Previous: Aan een spijker
KP Hart
2005-08-19
![]() die hierboven gevonden is is behoorlijk klein.
In dat geval kan
die hierboven gevonden is is behoorlijk klein.
In dat geval kan ![]() goed benaderd
worden met
goed benaderd
worden met
![]() (zie stukje over
(zie stukje over ![]() en
en ![]() in de vorige Pythagoras),
zodat
in de vorige Pythagoras),
zodat ![]() verandert in een bijna-gelijkheid:
verandert in een bijna-gelijkheid:
![]() is ook heel klein en voor heel kleine
is ook heel klein en voor heel kleine ![]() geldt
geldt
![]() ; daarmee kunnen we
; daarmee kunnen we ![]() omwerken tot
omwerken tot
![]() in.
Hoe groot is het verschil ten opzichte van het antwoord op de vorige opgave?
in.
Hoe groot is het verschil ten opzichte van het antwoord op de vorige opgave?
![]() is.
Vergelijk bijvoorbeeld
is.
Vergelijk bijvoorbeeld
![]() met
met ![]() ; voor welke
; voor welke ![]() is
het verschil klein genoeg om weg te laten?
Was in ons voorbeeld de benadering gerechtvaardigd?
is
het verschil klein genoeg om weg te laten?
Was in ons voorbeeld de benadering gerechtvaardigd?