


Next: About this document ...
Up: Logaritmen voor gevorderden
Previous: Gebruik van logaritmen
De ongelijkheid
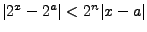
In het
januarinummer is aangetoond dat 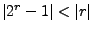 als
als 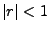 ;
met behulp hiervan bewijzen we de ongelijkheid hierboven.
;
met behulp hiervan bewijzen we de ongelijkheid hierboven.
We hebben ons getal 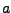 en gehele getallen
en gehele getallen 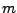 en
en 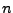 zó dat
zó dat 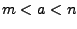 (met
(met 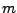 zo groot mogelijk en
zo groot mogelijk en 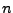 zo klein mogelijk).
Als nu
zo klein mogelijk).
Als nu 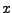 tussen
tussen 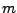 en
en 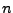 ligt dan geldt
ligt dan geldt 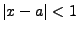 en dus
en dus
als 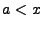 en
en
als 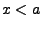 ; samengevat:
; samengevat:
als 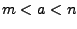 .
.
KP Hart
2006-12-05
![]() en gehele getallen
en gehele getallen ![]() en
en ![]() zó dat
zó dat ![]() (met
(met ![]() zo groot mogelijk en
zo groot mogelijk en ![]() zo klein mogelijk).
Als nu
zo klein mogelijk).
Als nu ![]() tussen
tussen ![]() en
en ![]() ligt dan geldt
ligt dan geldt ![]() en dus
en dus