


Next: De logaritme
Logaritmen voor gevorderden
Klaas Pieter Hart
Jaargang 45, April 2006
Abstract:
In het januarinummer van Pythagoras hebben we de functie
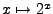
netjes
gedefinieerd.
In dit artikel kijken we naar de inverse functie: de logaritme.
De functie 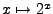 , zoals we die in het januarinummer hebben
gedefinieerd, heeft alle eigenschappen die we van een exponentiële functie
mogen verwachten.
De functie is strikt stijgend en voor alle
, zoals we die in het januarinummer hebben
gedefinieerd, heeft alle eigenschappen die we van een exponentiële functie
mogen verwachten.
De functie is strikt stijgend en voor alle 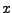 en
en 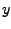 geldt
geldt
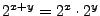 .
In dit artikel laten we zien dat onze functie een inverse functie heeft,
de logaritme in basis
.
In dit artikel laten we zien dat onze functie een inverse functie heeft,
de logaritme in basis 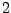 .
Die functie noteren we als
.
Die functie noteren we als 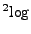 en per definitie betekenen
en per definitie betekenen
precies hetzelfde.
Bij het bepalen van een inverse functie verwisselen we domein en bereik:
het bereik/domein van 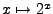 wordt het domein/bereik van
wordt het domein/bereik van
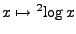 .
Het domein van
.
Het domein van 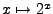 kennen we, dat is
kennen we, dat is 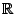 .
Het bereik kennen we nog niet; we weten dat de waarden in het interval
.
Het bereik kennen we nog niet; we weten dat de waarden in het interval
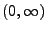 zitten maar wat we wilen, namelijk dat
zitten maar wat we wilen, namelijk dat 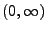 het domein
van de logaritme is, moeten we wel netjes vaststellen en dat doen
we door te bewijzen dat het bereik van
het domein
van de logaritme is, moeten we wel netjes vaststellen en dat doen
we door te bewijzen dat het bereik van 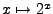 precies
het interval
precies
het interval 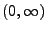 is.
is.
Dus bij gegeven 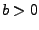 moeten we een
moeten we een 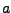 maken met
maken met 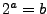 (en omdat
(en omdat 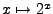 strikt stijgend is is er precies één zo'n
strikt stijgend is is er precies één zo'n 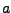 ).
Dit bewijzen we met behulp van de nu al vertrouwde eigenschap van
).
Dit bewijzen we met behulp van de nu al vertrouwde eigenschap van 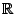 :
de volledigheid.
:
de volledigheid.



Next: De logaritme
KP Hart
2006-12-05
![]() , zoals we die in het januarinummer hebben
gedefinieerd, heeft alle eigenschappen die we van een exponentiële functie
mogen verwachten.
De functie is strikt stijgend en voor alle
, zoals we die in het januarinummer hebben
gedefinieerd, heeft alle eigenschappen die we van een exponentiële functie
mogen verwachten.
De functie is strikt stijgend en voor alle ![]() en
en ![]() geldt
geldt
![]() .
In dit artikel laten we zien dat onze functie een inverse functie heeft,
de logaritme in basis
.
In dit artikel laten we zien dat onze functie een inverse functie heeft,
de logaritme in basis ![]() .
Die functie noteren we als
.
Die functie noteren we als ![]() en per definitie betekenen
en per definitie betekenen
![]() moeten we een
moeten we een ![]() maken met
maken met ![]() (en omdat
(en omdat ![]() strikt stijgend is is er precies één zo'n
strikt stijgend is is er precies één zo'n ![]() ).
Dit bewijzen we met behulp van de nu al vertrouwde eigenschap van
).
Dit bewijzen we met behulp van de nu al vertrouwde eigenschap van ![]() :
de volledigheid.
:
de volledigheid.