Vergelijkingen oplossen

Heeft de vergelijking $\cos x=x$ een oplossing? Als je naar de grafieken van $y=\cos x$ en $y=x$ kijkt zou je zeggen van wel.

$$\includegraphics{tussenwaardestelling-1}$$

Bij $x=0$ ligt $x$ onder $\cos x$ (want $\cos 0=1>0$) en bij $x=1$ ligt $x$ boven $\cos x$ (want $\cos 1<1$). Je zou dus verwachten dat de grafieken elkaar tussen $0$ en $1$ kruisen en dat er dus een getal $a$ te vinden moet zijn met $\cos a=a$.

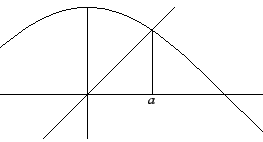
Om die verwachting in zekerheid om te zetten kunnen we twee dingen doen. We kunnen proberen de vergelijking op één of andere manier op te lossen en uit te komen op een uitspraak van de vorm $a=\ldots$; als je dat probeert zul je merken dat je eigenlijk geen houvast hebt en dat dit wellicht makkelijker gezegd is dan gedaan.

Het andere wat we kunnen doen is bewijzen dat zo'n $a$ moet bestaan en, als het even kan, een methode aangeven om goede benaderingen van die $a$ te maken.