Bewijzen dat $\cos a=a$

Om te bewijzen dat $\cos a=a$ hebben we een gonio-formule nodig: $\cos x-\cos a=-2\sin\bigl(\frac12 (x+a)\bigr)\sin\bigl(\frac12 (x-a)\bigr)$. Hieruit kunnen we afleiden dat $\cos x$ dicht bij $\cos a$ ligt als $x$ dicht bij $a$ ligt. De absolute waarde van het verschil is namelijk $2\bigl\vert\sin\bigl(\frac12 (x+a)\bigr)\bigr\vert \cdot\bigl\vert\sin\bigl(\frac12 (x-a)\bigr)\bigr\vert$, omdat een sinus nooit groter dan $1$ is kunnen we dit afschatten met $2\bigl\vert\sin\bigl(\frac12 (x-a)\bigr)\bigr\vert$. 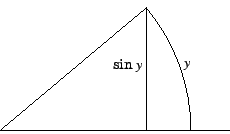Verder geldt altijd $\vert\sin y\vert\le y$, zie het plaatje.

$$\includegraphics{tussenwaardestelling-2}$$

We concluderen dat altijd

$$\vert\cos x-\cos a\vert\le\vert x-a\vert.$$

Hiermee kunnen we laten zien dat $\cos a\ge a$ en dat $\cos a\le a$ en dus dat $\cos a=a$.

Neem een willekeurig natuurlijk getal $n$ en kies $x\in A$ zó dat $x>a-2^{-n}$. We gaan het verschil $\cos a-a$ anders opschrijven, namelijk als de som van drie verschillen: $\cos a-\cos x$, $\cos x-x$ en $x-a$. Omdat $\vert\cos a-\cos x\vert\le\vert x-a\vert$ kunnen we afleiden dat de som van die drie verschillen groter is dan $-2\cdot2^{-n}$: $\cos x-x$ is positief en de andere twee termen zijn, in absolute waarde, niet groter dan $2^{-n}$. Dus, voor elke $n$ geldt $\cos a-a>-2\cdot 2^{-n}$. Maar dat betekent dat $\cos a-a$ tenminste zo groot is als de kleinste bovengrens van alle waarden $-2\cdot2^{-n}$ en dat is $0$. Conclusie $\cos a-a\ge0$.

Opgave. Laat met eenzelfde redenering zien dat $\cos a\le a$.