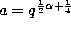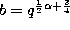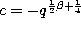, 
,
and 
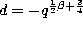in
the definition (3.1.1) of the Askey-Wilson polynomials we find
after renormalizing
Definition. If we take , ,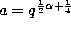
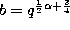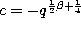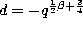and in
the definition (3.1.1) of the Askey-Wilson polynomials we find
after renormalizing
Orthogonality. For 
and 
we have
where
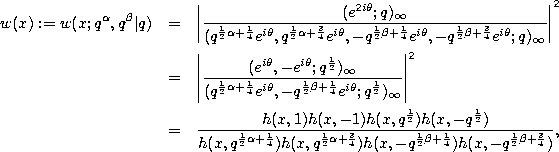
with
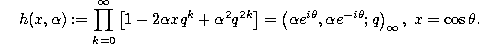
Recurrence relation.
where
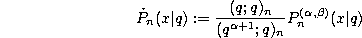
and
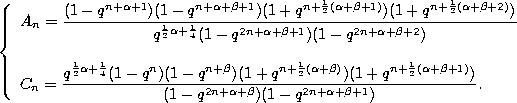
Normalized recurrence relation.
where
q-Difference equation.
where
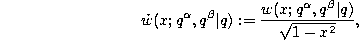
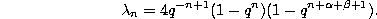
Forward shift operator.
or equivalently
Backward shift operator.
or equivalently
Rodrigues-type formula.
Generating functions.
Remarks. In [345] M. Rahman takes
, 
, 
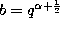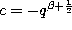and
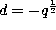in the definition (3.1.1) of the
Askey-Wilson polynomials to obtain after renormalizing
These two q-analogues of the Jacobi polynomials are not really different, since they are connected by the quadratic transformation :
The continuous q-Jacobi polynomials given by (3.10.14) and the continuous q-ultraspherical (or Rogers) polynomials given by (3.10.15) are connected by the quadratic transformations :
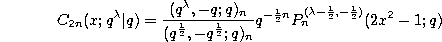
and
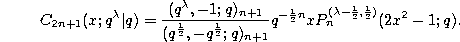
If we change q by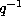 
we find
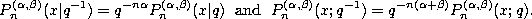
References. [64], [163], [191], [193], [232], [234], [237], [322], [323], [345], [347], [348], [350], [371], [389].
Definition. If we set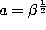 
, 
,
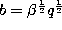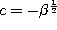and 
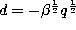in the definition
(3.1.1) of the Askey-Wilson polynomials and change the
normalization we obtain the continuous q-ultraspherical (or Rogers) polynomials :
Orthogonality.
where
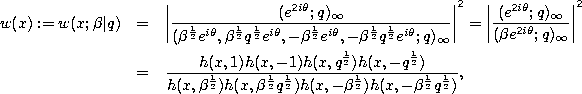
with
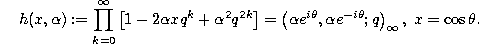
Recurrence relation.
Normalized recurrence relation.
where
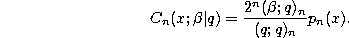
q-Difference equation.
where
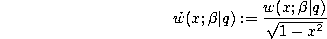
and
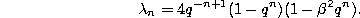
Forward shift operator.
or equivalently
Backward shift operator.
or equivalently
Rodrigues-type formula.
Generating functions.
Remarks. The continuous q-ultraspherical (or Rogers) polynomials can also be written as :
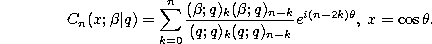
They can be obtained from the continuous q-Jacobi polynomials defined by
(3.10.1) in the following way. Set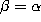 
in the definition
(3.10.1) and change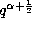 
by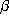 
and we find
the continuous q-ultraspherical (or Rogers) polynomials with a different
normalization. We have
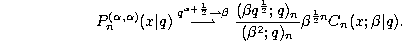
If we set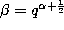 
in the definition (3.10.15) of
the q-ultraspherical (or Rogers) polynomials we find the continuous
q-Jacobi polynomials given by (3.10.1) with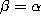 
. In
fact we have
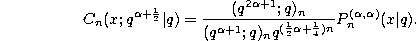
If we change q by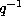 
we find
The special case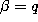 
of the continuous q-ultraspherical (or Rogers)
polynomials equals the Chebyshev polynomials of the second kind defined by
(1.8.31). In fact we have
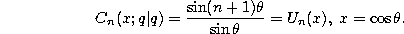
The limit case 
leads to the Chebyshev polynomials of the
first kind given by (1.8.30) in the following way :
The continuous q-Jacobi polynomials given by (3.10.14) and the continuous q-ultraspherical (or Rogers) polynomials given by (3.10.15) are connected by the quadratic transformations :
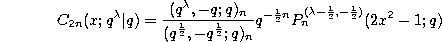
and
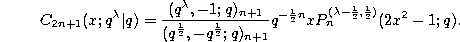
Finally we remark that the continuous q-ultraspherical (or Rogers) polynomials are related to the continuous q-Legendre polynomials defined by (3.10.32) in the following way :
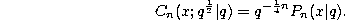
References. [13], [15], [16], [31], [43], [44], [45], [53], [54], [55], [57], [64], [67], [94], [98], [99], [165], [185], [186], [187], [189], [191], [192], [193], [218], [232], [238], [239], [243], [258], [259], [278], [322], [323], [327], [350], [352], [356], [357], [358], [363], [364], [365], [370].
Definition. The continuous q-Legendre polynomials are continuous
q-Jacobi polynomials with 
:
Orthogonality.
where
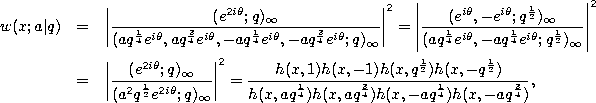
with
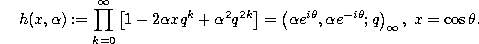
Recurrence relation.
Normalized recurrence relation.
where
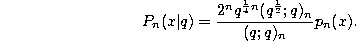
q-Difference equation.
where
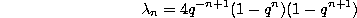
and
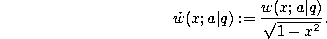
Rodrigues-type formula.
Generating functions.
Remarks. The continuous q-Legendre polynomials can also be written as :
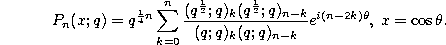
If we set 
in (3.10.14) we find
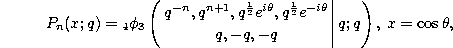
but these are not really different from those defined by (3.10.32) in view of the quadratic transformation
If we change q by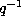 
we find
The continuous q-Legendre polynomials are related to the continuous q-ultraspherical (or Rogers) polynomials given by (3.10.15) in the following way :
References. [256], [262], [275], [279], [282].
