


Next: De formule van Stirling
Up: Hoe groot is ongeveer?
Previous: Afschatten
We kunnen 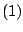 en
en 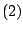 aanzienlijk verbeteren door met integralen
te werken.
Hiertoe nemen we de natuurlijke logaritme van
aanzienlijk verbeteren door met integralen
te werken.
Hiertoe nemen we de natuurlijke logaritme van 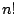 :
:
Deze som kunnen we vergelijken met een integraal van 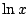 .
In figuur 1 is te zien dat
.
In figuur 1 is te zien dat
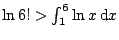 .
.
Figuur:
1
 |
In figuur 2 is te zien dat
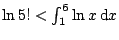 .
.
Figuur:
2
 |
In het algemeen krijgen we
Nu moeten we de integraal nog uitrekenen.
Daarvoor moeten we een primitieve van 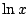 maken.
Met een beetje proberen kun je uitvlooien dat
maken.
Met een beetje proberen kun je uitvlooien dat
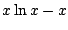 een primitieve is
(differentieer het om dat te controleren).
De integraal wordt dus
een primitieve is
(differentieer het om dat te controleren).
De integraal wordt dus
Dit kunnen we omwerken tot
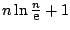 ,
ofwel
,
ofwel
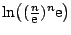 .
Conclusie:
.
Conclusie:
Hiermee vinden we
(vermenigvuldig de linker ongelijkheid in 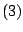 met
met 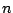 ).
).
Hiermee krijgen we zeer nauwkeurige grenzen voor ![$\sqrt[n]{n}$](img60.png) :
:
In het vorige nummer van Pythagoras hebben we gezien dat ![$\sqrt[n]{n}$](img60.png) naar
naar  daalt
(en
daalt
(en
![$\sqrt[n]{\mbox{e}}$](img63.png) dus ook);
daarmee zien we dat
dus ook);
daarmee zien we dat ![$\sqrt[n]{n!}$](img64.png) ongeveer net zo snel groeit als
ongeveer net zo snel groeit als
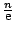 .
.



Next: De formule van Stirling
Up: Hoe groot is ongeveer?
Previous: Afschatten
KP Hart
2005-08-26
![]() en
en ![]() aanzienlijk verbeteren door met integralen
te werken.
Hiertoe nemen we de natuurlijke logaritme van
aanzienlijk verbeteren door met integralen
te werken.
Hiertoe nemen we de natuurlijke logaritme van ![]() :
:
![]() .
.
![]() :
: