Machtsverheffen voor gevorderden

Klaas Pieter Hart

Jaargang 45, Januari 2006

Abstract:

Wat is $2^{\sqrt3}$? In dit artikel gaan we precies afspreken wat $2^x$ is, voor alle reële getallen $x$.

In de vorige twee nummers van Pythagoras hebben we gezien waarom $n$-demachtswortels bestaan en hoe je die efficiënt kunt benaderen. Nu gaan de ons bezig houden met machtsverheffen; daar zitten ook nog een paar haken en ogen aan. Voor elk getal $x$ op de getallenlijn zullen we netjes definiëren wat $2^x$ betekent.

Om te beginnen voor natuurlijke getallen, daar is de betekenis duidelijk: voor een natuurlijk getal $n$ is $2^n$ een handige afkorting voor

$$\underbrace{2\times2\times\cdots\times2}_{n \mathrm{ maal}}$$

Voor willekeurige gehele getallen moeten we oppassen: we kunnen niet zonder meer afspreken dat

$$2^0=\underbrace{2\times2\times\cdots\times2}_{0 \mathrm{ maal}}$$

en

$$2^{-10}=\underbrace{2\times2\times\cdots\times2}_{-10 \mathrm{ maal}}$$

want die twee dingen betekenen natuurlijk niks.

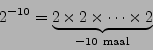
De juiste afspraak voor $2^0$, $2^{-1}$, $2^{-2}$, ...$2^{-10}$, ... komt voort uit de wens een mooie eigenschap van de notatie $2^n$ in stand te houden, namelijk

$$2^m\times 2^n=2^{m+n}\eqno(*)$$

Voor $m=0$ zou hier $2^0\times 2^n=2^n$ staan en dat betekent dat $2^0=1$ de enig juiste afspraak is. Omdat $1-1=0$ volgt nu dat $2^{-1}$ zó gekozen moet worden dat $2\times 2^{-1}=1$ en dus $2^{-1}=\frac12$. Evenzo volgt $2^{-2}=\frac14$, ..., $2^{-10}=\frac1{1024}$, ...

Opgave. Ga na dat de eigenschap $2^m\times 2^n=2^{m+n}$ inderdaad bewaard blijft voor negatieve en positieve $m$ en $n$.